Длина периода

• Удачный выбор параметров даёт известную и достаточно большую длину периода.
• неудачный выбор сделать проще
• например, \(a=1, c=1\), даст счётчик

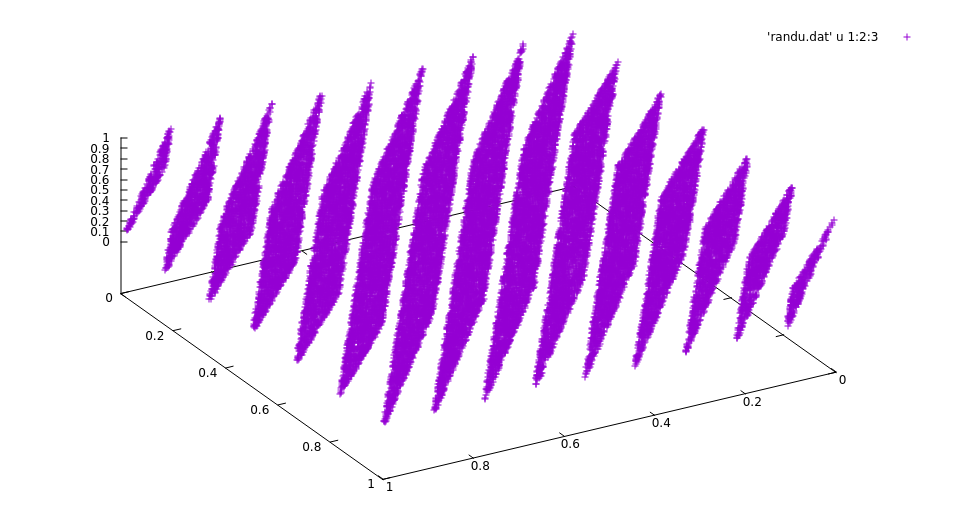
• пример – генератор RANDU,
• \(a=65539=2^{16}+3, c=0, m=2^{31}\)
• равномерно распределённые значения
• не независимые

• каждое третье однозначно определяется двумя предыдущими
• это уравнение 3-мерной плоскости
• (технически, из-за \(\mod 2^{31}\) – семейство 15 плоскостей)
• каждая тройка лежит на этой плоскости

Выбор параметров

• Три варианта:
• \(m\) – простое, \(c=0\)
• \(m=2^n\), \(c=0\)
• \(c\neq 0\)

\(m\) простое, \(c=0\)

• генератор Лемера
• Если \(a\) – примитивный элемент группы по модулю \(m\), период равен \(m-1\)
• \(s_0\neq 0\)
• \(m\) – часто числа Мерсенна \(M_n=2^n-1\), например \(2^{31}-1\) или \(2^{61}-1\).

• при использовании двоичной арифметики, необходим явный шаг вычисления остатка, и двойной объем памяти при умножении.
• если необходимо получить РРСП бит, числа в \([1,m)\) не всегда легко преобразовать.

• Вычислим \(a\cdot s\)
• Пусть \(m = qa+r,\) \(q = \floor{\frac{m}{a}}\), \(r = m \mod a\)
• \(a\cdot s \mod m = a\cdot(s \mod q) − r \floor{\frac{s}{q}}\)

• если \(r \le q\), то

• оба члена можно вычислить в том же числе разрядов, что и \(m-1\)
• разность лежит в \([1−m, m−1]\), легко привести к диапазону \([0, m−1]\)

\(m=2^n\), \(c=0\)

• при использовании двоичной арифметики в \(n\) разрядах, вычисление резко упрощается.
• обратная сторона: младшие биты менее случайные, чем старшие

• Возьмём ЛКГ \(s_{i+1} = as_i \mod 2^n\)
• рассмотрим младшие \(l\) бит состояния: \(t_i = s_i \mod 2^l.\)
• \(t_{i+1} = (as_i \mod 2^n) \mod 2^l\)
• \(t_{i+1} = at_i \mod 2^l,\)
• образуют ЛКГ с меньшим периодом
• в лучшем случае, младший бит никогда не меняется, второй по старшинству бит меняется каждый раз, и т.д.

\(c\neq 0\)

• длина периода может достигать \(m\)

Лемма 1

Пусть \(p\) – простое число, а \(e\in\mathbb N: p^e > 2\).

• По условию, \(\exists q\in \mathbb N: x = 1 + qp^e\)
• Тогда \(x^p = 1 + C_p^1 qp^e + \ldots + C_p^{p-1}q^{p-1}p^{e(p-1)}+q^pp^{ep},\)
• \(C_n^k = \frac{n!}{k!(n-k)!}\) – биномиальный коэффициент.

\[x^p = 1 + qp^{e+1}(1 + C_p^2 q p^{e-1} \\+ \ldots + C_p^{p-1}q^{p-2}p^{e(p-2)-1}+q^{p-1} p^{e(p-1)-1})\]

• \(C_p^k q^{k-1} p^{e(k-1)-1}\mod p^{e(k-1)} = 0\) для \(1<k<n\)
• \(q^{p-1} p^{e(p-1)-1} \mod p = 0\) т.к. \(e(p-1) > 1\) при \(p^e>2\)
• все члены в скобках кроме \(1\) делятся на \(p\)
• \(x^p = 1 \mod p^{e+1}.\)
• \(x^p = 1+qp^{e+1} \mod p^{e+2}.\qed\)

Следствие

По индукции,

Лемма 2

Пусть \(m\) раскладывается на простые множители \[m=p_1^{e_1} \ldots p_t^{e_t}.\]

Тогда длина периода \(\lambda\) ЛКГ, с параметрами \((s_0, a, c, m)\) – НОК длин \(\lambda_j\) периодов ЛКГ \((s_0 \mod p_j^{e_j}, a \mod p_j^{e_j}, c \mod p_j^{e_j}, p_j^{e_j})\), \(1 \le j \le t\).

• Докажем для \(G=(s_0, a, c, m_1m_2)\), где \(m_1\) и \(m_2\) – взаимно простые. Остальное очевидно верно по индукции по \(t\)
• Рассмотрим \(G_1 = (s_0 \mod m_1, a \mod m_1, c \mod m_1, m_1)\)
  \(G_2=(s_0 \mod m_2, a \mod m_2, c \mod m_2, m_2)\)
• \(g^{(1)}_n = g_n \mod m_1\)
• \(g^{(2)}_n = g_n \mod m_2\)
• Тогда \(\forall k\), \(g_n = g_k \mod m_1m_2 \iff\) \(g^{(1)}_n = g^{(1)}_k \mod m_1,\) \(g^{(2)}_n = g^{(2)}_k \mod m_2.\)

• пусть \(λ=λ(G),\) \(λ_1=λ(G_1)\), \(λ_2=λ(G_2)\)
• пусть \(\lambda'=\)НОК\((\lambda_1, \lambda_2\)).
• Т.к. \(\forall n>n_0:~ g_n = g_{n+\lambda}\), то \(g^{(1)}_n = g^{(1)}_{n+\lambda}\) и \(g^{(2)}_n = g^{(2)}_{n+\lambda}\),
• следовательно, \(\lambda\) – общее кратное \(\lambda_1\) и \(\lambda_2\),
• следовательно, \(\lambda \ge \lambda'\).
• С другой стороны, \(g^{(1)}_n = g^{(1)}_{n+\lambda_1}\) и \(g^{(2)}_n = g^{(2)}_{n+\lambda_2}\) для достаточно больших \(n\) и следовательно \(g_n = g_{n+\lambda'}\), и тогда \(\lambda \le \lambda'\).
• \(λ=λ'\qed\)

Теорема Халла-Добелла

ЛКГ, задаваемый рекуррентным соотношением \[s_{i+1} = a s_i + c \mod m,\] \(c \neq 0\) достигает периода \(m\) iff:

1. \(m\) и \(c\) взаимно простые
2. \(a=1\mod p\) для всех \(p\) – простых делителей \(m\)
3. \(a=1\mod 4\), если \(m\) делится на 4.

• для \(a=1\) и взаимно простых \(m\) и \(c\), период тривиально \(m\). Далее рассматриваем \(a>1\).

• \[s_1 = as_0+c\mod m\]

  \[s_2 = a(as_0+c)+c\mod m\]

  \[s_2 = a^2s_0+ac+c\mod m\]

  \[s_3 = a(a^2s_0+ac+c)+c\mod m\]

  \[s_3 = a^3s_0+a^2c+ac+c\mod m\]

  \[s_n = a^n s_0+c\sum_{i=0}^{n-1}a^i\mod m\]

  \[s_n = a^n s_0+c\frac{a^n-1}{a-1}\mod m\]

• Поскольку период \(m\) для последовательности \(\mod m\) пробегает все значения, БОО можем взять \(s_0=0\), т.е. \(s_n = c \frac{a^n-1}{a-1} = 0\mod m\)
• Мы хотим найти наименьшее \(λ\) такое, что \(s_λ=s_0=0\mod m\)

• Если \(c\) и \(m\) не взаимно простые, то \(s_n\) не может быть равно 1, ни для каких \(n\) и период меньше \(m\).
• Если \(c\) и \(m\) взаимно простые, то \[s_λ=0\iff\frac{a^λ-1}{a-1} = 0\mod m\]
• По лемме 2, достаточно доказать теорему для \(m=p^e\), т.к. \[m=p_1^{e_1}\ldots p_t^{e_t}=λ=lcm(λ_1,\ldots,λ_t),\] \[lcm(λ_1,\ldots,λ_t)\leλ_1\ldotsλ_t\le p_1^{e_1}\ldots p_t^{e_t},\] что возможно только если \(λ_i=p_i^{e_i}\)

• положим \(m=p^e\), где \(p\) – простое
• для \(a=1\) теорема тривиально верна. Далее считаем \(a>1\)
• пусть \(p>2\), тогда (3) условие опускается, и теорема сводится к утверждению \[\min\brace{λ:\frac{a^λ-1}{a-1} = 0\mod p^e}=p^e\\\iff a=1\mod p\]

\[\min\brace{λ:\frac{a^λ-1}{a-1} = 0\mod p^e}=p^e\\\iff a=1\mod p\]

• Докажем необходимость.
• Пусть \(\lambda=p^e\) и при этом \(a\neq 1 \mod p\).
• Тогда \(a^\lambda = 1 \mod p^e,\)
• по теореме Ферма \(a^n = a \mod n\)
• противоречие

• докажем необходимость (3)
• пусть \(p=2\)
• из (2), \(a=1\mod 2\)
• если \(a \neq 1 \mod 4\), то ввиду (2) \(a=3\mod 4\), \(a=3+4q\)
• \(\forall e>1:\:a\neq 1 \mod 2^e\)
• Тогда \(a^\lambda = 1 \mod p^e,\)
• по теореме Ферма \(a^n = a \mod n\)
• противоречие

• Докажем достаточность
• из (2,3) следует \(a=1+qp^f\)
• Применяя следствие леммы 1, \(\forall g\ge 0\)

• это верно и для \(g=e\).

• осталось показать, что \(λ=p^e\) минимально
• рассмотрим генератор \((0,a,1,p^e)\)
• для него верно \(s_n=\frac{a^n-1}{a-1}\mod p^e\). Его период \(λ\). \(s_n=0\) iff \(n\) кратно \(λ\).
• т.к. \(\frac{a^{p^e}-1}{a-1} = 0 \mod p^{e},\) то \(p^e\) кратно \(λ\)
• но \(\frac{a^{p^{e-1}}-1}{a-1} \neq 0 \mod p^{e}\)
• следовательно, \(λ=p^e\) минимально \(\qed\)

Следствия теоремы

• Из доказательства прямо следуют выражения максимального периода для \(c=0\).
• \(c=0 \Rightarrow s_n = a^n s_0 \mod m\).
• По лемме 2, период любого ЛКГ зависит от длин последовательностей при \(m=p^e\).
• Если \(s_n = a^n s_0 \mod p^e,\) и \(a\) кратно \(p\), период будет иметь длину не более \(e\)

• Рассмотрим случай, когда \(a\) и \(p\) – взаимно простые. Тогда \(\lambda\) – наименьшее число: \(s_0 = a^\lambda s_0 \mod p^e.\)
• Если теперь \(p^f = lcm(s_0, p^e)\), то это эквивалентно \(a^\lambda = 1 \mod p^{e-f}.\)
• По теореме Эйлера, \(a^{\varphi(m)} = 1 \mod m\), поэтому \(\lambda\) является делителем \(\varphi(p^{e-f})\), \(\varphi(p^{e-f}) = p^{e-f-1}(p-1).\)
• Eсли \(s_0\) и \(p^e\) взаимно простые, то \(p^f=1\), \(f=0\) и \(\varphi(p^{e}) = p^{e-1}(p-1).\)

Это позволяет определить \(\lambda(m)\): \[\lambda(m) = \begin{cases} 1, && m=2 \\ 2, && m=4 \\ 2^{e-2}, && m=2^e, e\ge3 \\ p^{e-1}(p-1), && m=p^e, p>2 \\ lcm(\lambda(p_1^{e_1}),\ldots,\lambda(p_n^{e_n})), && m = p_1^{e_1}\ldots p_n^{e_n} \end{cases}\]

Теорема

Максимальным периодом ЛКГ \((s_0,a,0,m)\) является \(\lambda(m)\). Этот период достигается, если:

1. \(s_0\) и \(m\) – взаимно простые
2. \(a\) является первообразным элементом мультипликативной группы по модулю \(m\).