Нелинейные генераторы ПСЧ
Инверсный конгруэнтный метод
- нелинейный генератор ПСЧ
- состояние вычисляется как линейная функция от обратного (по модулю) к текущему.
- \(s_{i+1} = \begin{cases} as_i^{-1}+c \mod p, && s_i\neq 0\\ c \mod p, && s_i = 0\\ \end{cases}\),
\(p\) – простое.
- Максимальный – \(p\)
- достигается если \(f(z) = z^2 - cz - a\) – примитивный в поле \(GF(p)\)
- \(f(z)\) примитивный, если \(f(z) = (z-\alpha)(z-\alpha^p),\)
- \(\alpha\) – примитивный элемент \(GF(p^2)\)
- тогда
\(c = \alpha + \alpha^p \mod p\)
\(a = - \alpha^{p+1} \mod p\)
- отсутствуют линейные корреляции между идущими подряд числами
- отсутствует характерная для ЛКГ “решетчатая” структура
- не отменяет наличия других корреляций.
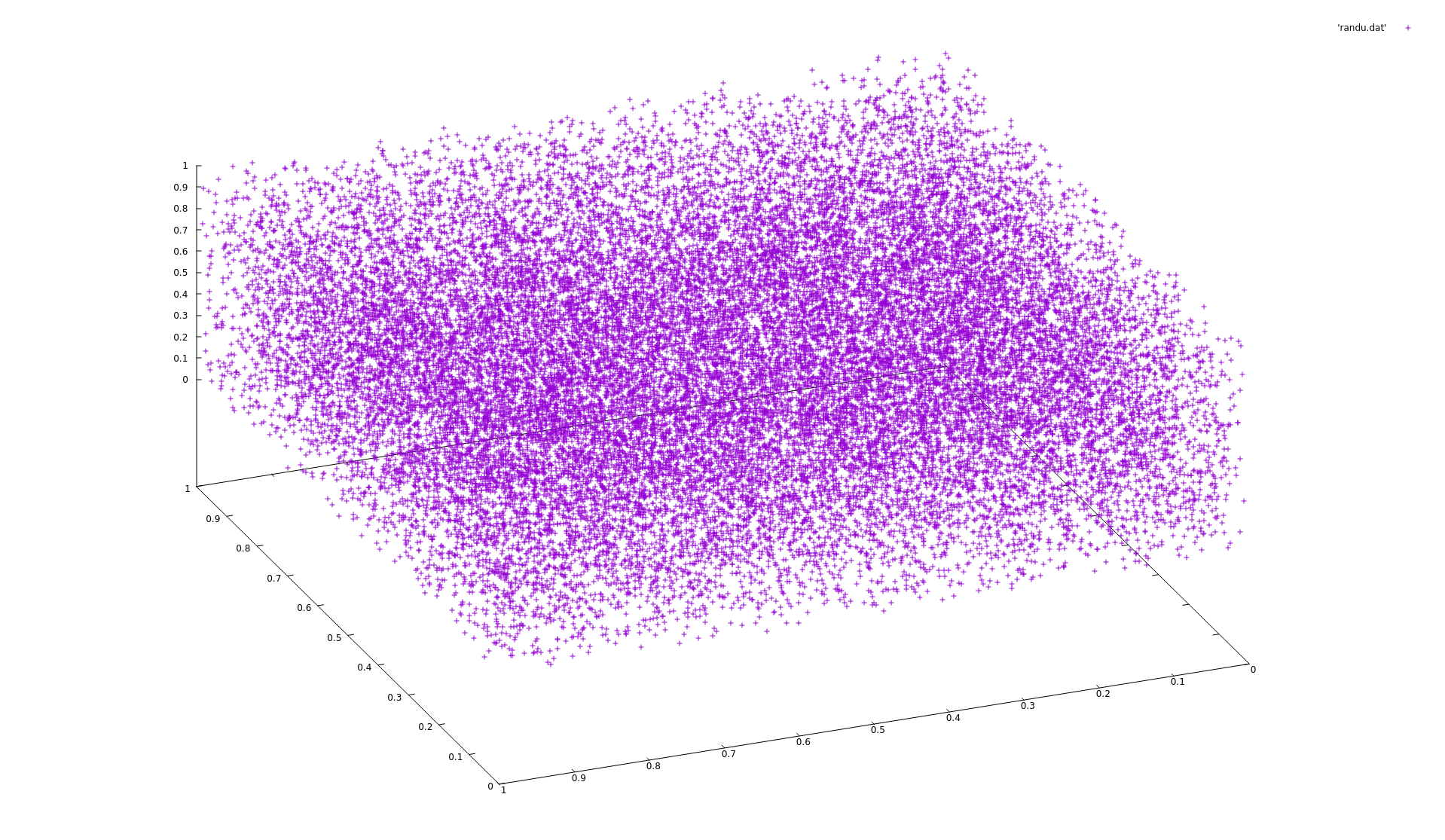
Метод умножения с переносом
- специальный случай генератора Лемера
- эффективное использование в качестве модуля \(p\) чисел, больших машинного слова
- \(x_n = (ax_{n-r}+c_{n-1}) \mod b,\)
- \(c_{n} = \floor{\frac{a x_{n-r}+c_{n-1}}{b}}\) – перенос
- \(a\) – множитель
- \(b\) – база
- состояние \(s_{n-1}\) – \(r\) значений \(x_{n-r}, \ldots, x_{n-1}\) и \(c_{n-1}\)
- Пусть \(p = ab^{r}-1\)
- состояние представим как \(b\)-ичное целое \(s_{n-1} = \overline{c_{n-1}x_{n-1}\ldots x_{n-r}}\)
- Тогда шаг представляется как:
- \(s' = s_{n-1} - x_{n-r}\)
- \(s'' = s' + a x_{n-r} b^r\)
- \(s_n = \floor{s''/b}\)
\(s_n = \floor{s''/b}\)
\(s_n = \floor{\frac{s' + a x_{n-r} b^r}{b}}\)
\(s_n = \floor{\frac{s_{n-1} - x_{n-r} + a x_{n-r} b^r}{b}}\)
\(s_n = \floor{\frac{c_{n-1}b^r + x_{n-1}b^{r-1}+\ldots+x_{n-r+1}b + x_{n-r} - x_{n-r} + a x_{n-r} b^r}{b}}\)
\(s_n = \floor{\frac{c_{n-1}b^r + x_{n-1}b^{r-1}+\ldots+x_{n-r+1}b + a x_{n-r} b^r}{b}}\)
\(s_n = c_{n-1}b^{r-1} + x_{n-1}b^{r-2}+\ldots+x_{n-r+1} + a x_{n-r} b^{r-1}\)
\(s_n = (c_{n-1}+ a x_{n-r})b^{r-1} + x_{n-1}b^{r-2}+\ldots+x_{n-r+1}\)
\(s_n = \floor{(c_{n-1}+ a x_{n-r})/b}b^r + (c_{n-1} + a x_{n-r}\mod b)b^{r-1} \\+ x_{n-1}b^{r-2}+\ldots+x_{n-r+1}\)
- (1-2) соответствуют \(s'' = s_{n-1} + x_{n-r}(a b^r - 1) = s_{n-1} + x_{n-r}p\)
- (3) соответствует \(s_{n} = s'' b^{-1}\mod p\)
- эквивалентен генератору Лемера \(s_n = s_{n-1} b^{-1} \mod p\)
- Период – порядок \(b\) в мультипликативной группе по модулю \(p\).
- Часто выбирается “безопасное” простое \(p\), \(p=2q+1\), где \(q\) простое.
- По теореме Ферма, порядок любого элемента есть делитель \(p-1\)
- период – делитель \(2q\)
- пусть \(b\neq p-1\) (единственный элемент с порядком 2)
- \(\lambda = q = (p-1)/2 = ab^r/2 − 1\).
Односторонние функции
- Односторонняя функция
- Функция \(f:X\to Y: \exists \mathcal A\) – алгоритм вычисления \(f(x)\) за полиномиальное время. При этом, \[\forall F, \forall c \in \mathbb N : \mathrm P[f(\mathcal F(f(x))) = f(x)] < |x|^{-c},\] где \(|x|\) – размер аргумента (в каком-либо смысле), \(P\) – вероятность, \(\mathcal F\) – рандомизированный полиномиальный по времени алгоритм.
- Т.е. не существует алгоритма \(\mathcal F\) вычисляющего \(f^{-1}\) с вероятностью лучшей, чем случай.
- определение требует отсутствия полиномиального алгоритма обращения функции для усреднённого случая
- резко отличает от теории сложности, где рассматривается, как правило, худший случай
- даже если задача обращения – NP-сложная, это не гарантирует, что функция – односторонняя.
- для односторонней функции недостаточно сделать её “теряющей информацию”
- \(f(x) = 0\) не позволяет восстановить исходное \(x\), но позволяет легко подобрать другое \(x : f(x) = 0\)
- Существование односторонних функций формально не доказано
- Доказательство их существования докажет неравенство классов P и NP
- Современная асимметричная криптография основывается на предположении о существовании односторонних функций
Кандидаты в односторонние функции
Умножение и факторизация
- \(f(p,q) = p\cdot q\)
- сложность \(O(b^2)\), где \(b\) – число бит во входных числах
- обратная ф-я – факторизация
- лучшие известные алгоритмы имеют сложность \(O\paren{\exp\sqrt[3]{\frac{64}{9}b(\log b)^2}}\), где \(b\) – число бит факторизуемого числа.
- \(f\) не является односторонней для случайных \(p\), \(q\). Половина всех чисел – чётные. Вероятность \(p\) и \(q\) оба нечётные – ¼. ¾ всех чисел будут иметь фактор 2.
- алгоритм Шора – факторизация за полиномиальное время на квантовом компьютере.
Функция Рабина (квадрат по модулю)
- \(f_{pq} (x) = x^2 \mod pq,\) \(p,\) \(q\) – простые.
- \(f^{-1}\) эквивалентна факторизации – сводится за полиномиальное время
- Функция Рабина односторонняя iff умножение простых одностороннее.
Дискретное возведение в степень и логарифм
- \(f(x) = a^x \mod p\) вычисляется за полиномиальное время
- \(f^{-1}\) – дискретный логарифм.
- Существуют конечные абелевы группы, для которых неизвестны полиномиальные алгоритмы вычисления дискретного логарифма.
Популярные варианты:
- мультипликативная группа над конечным полем целых чисел по простому модулю
- циклические подгруппы на эллиптических кривых над конечными полями
- алгоритм дискретного логарифмирования Шора – полиномиальное время на квантовом компьютере.
Криптографически безопасные хэш-функции
- Существуют “легко” вычислимые криптографические хэш-функции
- более простые алгоритмы имеют слабые места (MD5, SHA1)
- многие остаются практически безопасными и не имеют “лёгких” алгоритмов обращения.
Случайные линейные коды
- любопытный кандидат в односторонние функции
- задача кодирования-декодирования случайным линейным кодом
- задача кодирования в худшем случае полиномиально сложная от размера блока
- задача декодирования – экспоненциально сложная от размера блока
Криптостойкие ГПСЧ на односторонних функциях
- Идея – использовать одностороннюю функцию
- умножение
- возведение в степень
ГПСЧ Шамира
- Выбрать \(p\) и \(q\) – простые. Вычислить \(n=pq\) и \(m=(p-1)(q-1)\). Выбрать случайное целое \(1<e<m\), взаимно простое с \(f\).
- Выбрать случайное начальное состояние \(1 \le s_0 \le n-1\)
- \(s_i = s_{i-1}^e \mod n\)
- Вывод \(x_i = s_i \mod 2\)
- \(\exists\) более эффективные модификации, напр., алг. Микали-Шнорра
ГПСЧ Блюма-Микали
- Выбрать \(g\) и \(p\), причём \(g\) – примитивный элемент мультипликативной группы по модулю \(p\), \(p\) – простое.
- Выбрать случайное начальное состояние \(1 < s_0 < p-1\)
- \(s_{i+1} = g^{s_i} \mod p\)
- Вывод \(x_i = \left\lbrace\begin{align} 1, && s_{i} < (p-1)/2 \\ 0, && s_{i} \ge (p-1)/2 \\ \end{align}\right.\)
ГПСЧ Блюм-Блюма-Шуба
- Выбрать простые числа \(p\) и \(q\), конгруэнтные 3 по модулю 4, причём такие, что \(gcd(\phi(p-1),\phi(q-1))\) мал (\(\phi\) – ф-я Эйлера). Вычислить \(n=pq\).
- Выбрать начальное состояние \(s_0 > 1\), взаимно простое с \(n\).
- \(s_{i+1} = s_i^2 \mod n\)
- Вывод \(x_i = s_i \mod 2\)
- Вообще говоря, вывод не обязательно по модулю 2.
- Интересное свойство – можно прямо вычислить \(s_i\) по теореме Эйлера: \(s_i = s_0^{2^i \mod \lambda(n)} \mod n.\)
- Здесь \(\lambda\) – функция Кармайкла, \(\lambda(n) = \min \{m | \forall a\in\mathbb N, 1<a<n-1 : a^m = 1 \mod n\}.\)
- В данном случае, \(\lambda(n) = \lambda(pq) = lcm(p-1,q-1)\) (мы получили аналогичный результат в виде леммы 2 при доказательстве теоремы Халла-Добелла)
Генерация случайных простых чисел
- основана на т-ме Чебышева: \(\forall n\in\mathbb N, n \ge 2: \exists\) простое \(p \in \brack{n, 2n}\)
- Ввод: натуральное число \(N\ge 2\)
- Вывод: случайное простое число из \((N,2N)\)
- \(P\gets\) случайное число из \((N,2N)\)
- Если \(P\) чётное, \(P\gets P+1\)
- Пока \(P\) составное
- \(P\gets P+2\)
- Если \(P\ge 2N\) то \(P\gets N+1\), перейти к 2.
- Конец
Детерминированные тесты простоты
Тест Агравала-Каяла-Саксены
- универсальный полиномиальный, детерминированный, безусловный
- основан на обобщении малой теоремы Ферма на многочлены
- пространственная сложность в худшем случае – крайне высока
- практически не применяется
Тест Адлемана-Померанса-Румели
- эффективный, детерминированный, безусловный
- разработан в 1983 году
- улучшен Генри Коэном и Хендриком Ленстрой (APR-CL)
- временная сложность улучшенного алгоритма \(O((\ln n)^{c\,\ln \,\ln \,\ln n}),\) где \(c\) — некоторая константа.
Тест Аткина-Морейна на эллиптических кривых (ECPP)
- Универсальный алгоритм
- В настоящее время самый быстрый практический алгоритм
- Сложность в худшем случае – неизвестна
- Эвристическая оценка временной сложности составляет \[O((\log n)^{6+\varepsilon })\] для некого \(\varepsilon>0\).
Вероятностные тесты простоты
Тест Миллера-Рабина
- Основное утверждение теста
Пусть \(n\) — простое число и \(n-1=2^{s}d\), где \(d\) — нечётно. Тогда для любого \(a \in \mathbb N\), \(0 < a < n\) выполняется хотя бы одно из условий:
- \(a^{d} = 1 \pmod {n}\)
- \(\exists r \in \mathbb N_0, r < s:\) \(a^{2^{r}d} = -1\pmod {n}\)
- Идея: если хотя бы одно из условий выполняется для чисел \(a\) и \(n\), то \(a\) называется свидетелем простоты по Миллеру
- Если найдётся число, для которого оба условия не выполняются, то \(n\) – составное.
- Рабин доказал, что у нечётных составных \(n\) не более \(\varphi(n)/4\) свидетелей простоты.
- Для составного числа вероятность случайно выбрать свидетеля простоты не больше ¼.
- Тогда \(k\) раз случайно выбирая различные \(a<n\), если все они окажутся свидетелями простоты, вероятность того, что \(n\) составное не больше \(2^{-2k}\).
- сложность алгоритма \(O(k \log^3 n)\)
Тест Соловея — Штрассена
- Основное утверждение теста
- Если \(n\) – нечётное составное число, то количество целых чисел \(a\), взаимно простых с \(n\) и меньших \(n\), удовлетворяющих соотношению \(a^{(n-1)/2} = \paren{\frac{a}{n}} \pmod n,\tag{*}\) не превосходит \(n/2\), где \(\paren{\frac{a}{n}}\) – символ Якоби.
\(\left(\frac{a}{n}\right) = \left(\frac{a}{p_1}\right)^{\alpha_1}\left(\frac{a}{p_2}\right)^{\alpha_2}\cdots \left(\frac{a}{p_k}\right)^{\alpha_k},\) где \(n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}\) – разложение \(n\) на простые множители, а \(\left(\frac{a}{p}\right) = \begin{cases} 0, & a = 0 \pmod{p},\\ 1, & a \neq 0\pmod{p}, \exists x \in \mathbb N :a= x^2\pmod{p},\\ -1, & \text{otherwise} \end{cases}\) \(\left(\frac{a}{1}\right) = 1.\)
- Идея – провести \(k\) проверок утверждения теста
- В каждом раунде случайным образом выбирается число \(a < n\). Если \(gcd(a,n) > 1,\) то n – составное.
- Иначе, проверяется справедливость \((\text{*})\), если оно не выполняется, то \(n\) — составное.
- Если выполняется, то \(a\) – свидетель простоты \(n\).
- При \(k\) свидетелях простоты, \(n\) является составным с вероятностью \(2^{-k}.\)
- Асимптотическая сложность практически такая же, как у теста Миллера-Рабина
- Тест Миллера-Рабина даёт лучшую вероятность за меньшее число итераций
Вычисление символа Якоби
Алгоритм, аналогичный алгоритму Евклида
Свойства \(\paren{\frac{a}{n}}\):
- Если \(a = b \pmod n\), то \(\paren{\frac{a}{n}} = \paren{\frac{b}{n}}\)
- \(\paren{\frac{2a}{n}} = \paren{\frac{2}{n}} \paren{\frac{a}{n}}\), \(\paren{\frac{2a}{n}} = \begin{cases} \paren{\frac{a}{n}}, & n = 1, 7 \pmod 8 \\ -\paren{\frac{a}{n}}, & n = 3, 5 \pmod 8 \\ \end{cases}\)
- \(\paren{\frac{ab}{n}} = \paren{\frac{a}{n}}\paren{\frac{b}{n}}\)
- \(\paren{\frac{a}{n}} = \begin{cases} 0, & gcd(a,n) \neq 1 \\ \pm 1, & gcd(a,n) = 1 \end{cases}\)
- Если \(n>0\), \(m>0\), \(gcd(m,n) = 1\), то \(\paren{\frac{m}{n}} \paren{\frac{n}{m}} = (-1)^{\frac{1}{4}(m-1)(n-1)}=\begin{cases} -1, & n = m = 3 \pmod 4 \\ 1, & \text{otherwise} \end{cases}\)
Алгоритм
- \(a \leftarrow a \mod n\) (по св-ву 1)
- Если \(a\) чётное, преобразовать по св-ву 2: \(\paren{\frac{2a}{n}} = \paren{\frac{2}{n}} \paren{\frac{a}{n}}\)
- Если \(a = 1\), то вернуть \(1\) (по св-вам 3,4)
- Если \(gcd(a,n) \neq 1\), то вернуть 0 (по св-ву 4)
- По свойству 5, поменять \(a\), \(n\) местами: \(\paren{\frac{a}{n}}=\begin{cases} -\paren{\frac{n}{a}}, & n = a = 3 \pmod 4 \\ \paren{\frac{n}{a}}, & \text{otherwise} \end{cases}\)
- перейти к шагу 1.
Алгоритм Евклида
- достаточно эффективный поиск НОД
- Пусть ищется \(gcd(a,b)\), \(a > b\)
- Тогда можно построить последовательность \(r_0 > r_1 > r_2 > \ldots > r_n > 0\), таких, что \(r_0 = a\), \(r_1 = b\), \(\ldots\), \(r_i = r_{i-2} - r_{i-1}q_{i-1}\), \(\ldots\), где \(q_i = \floor{\frac{r_{i-2}}{r_{i-1}}}\)
- Тогда \(gcd(a, b) = r_n\)
- Расширенный алгоритм Евклида дополнительно вычисляет последовательности \(s_i\) и \(t_i\):
- \(s_0=1\), \(s_1=0\), \(s_i = s_{i-2}-q_{i-1} s_{i-1}\)
- \(t_0=0\), \(t_1=1\), \(t_i = t_{i-2}-q_{i-1} t_{i-1}\)
- \(s_n\) и \(t_n\) дают коэффициенты Безу: \(r_n = as_n + bt_n\)
- можно использовать для вычисления мультипликативно-обратного.
- Чтобы \(a^{-1}\mod m\) существовало, \(gcd(a, m) = 1\). Тогда \(ms_n + at_n = gcd(a,m) = 1,\) ⇒ \(at_n = -ms_n + 1,\) ⇒ \(at_n = 1 \pmod m,\)
- \(t_n = a^{-1} \mod m\)