Часть 0. Введение
Введение. О проблеме транспортных перевозок в Арктике и на Дальнем Востоке
В освоении арктических регионов РФ значительна роль транспортной проблемы [1]. Если в среднем по стране доля транспортных расходов в себестоимости продукции составляет 10…12%, то на Севере она может достигать 30…60% и более.
В Северной и Азиатской части России, особенно в ее Арктической зоне, крупные железнодорожные и автомобильные магистрали имеются только в южных регионах и ориентированы в направлении «восток-запад». Транспортные перевозки в меридиональных направлениях крайне затруднены. Особенно остро эти затруднения проявляются в зимний период, что вызывает необходимость организации т.н. «северного завоза».
Природно-климатические и экономические особенности Арктических регионов РФ определяют особый подход к формированию транспортной системы Арктики.
Среди основных влияющих факторов:
- низкая плотность населения (до 0,3 чел./км2), большие расстояния между малыми населёнными пунктами, что определяет относительно небольшие пассажиропотоки.
- преимущественно очаговая деятельность при освоении сырьевых месторождений;
- суровые климатические условия (годовой ход температур наружного воздуха в отдельных регионах достигает 100°), короткое лето, полярная ночь;
- наличие вечной мерзлоты, значительного количества болот, рек, озер;
- экологическая уязвимость северных экосистем;
- повышенный уровень цен на все виды топлива, оборудование и товары в результате разового завоза из центра страны и хранения межсезонных запасов;
- более высокая (в 7…10 раз) стоимость создания и эксплуатации традиционной транспортной инфраструктуры;
- слабое развитие наземных транспортных коммуникаций.
Освоение минерально-сырьевых и природных ресурсов Арктики, Сибири и Дальнего Востока настоятельно требует создания адекватной транспортной системы.
Для большинства осваиваемых месторождений характерен типовой жизненный цикл «разведка – освоение – эксплуатация – свертывание» длительностью от нескольких лет до нескольких десятков лет. Как правило, добывающие компании не заинтересованы в развитии капитальных транспортных сетей, и предпочитают использовать экологически неблагополучные, малоэффективные и дорогие в эксплуатации гусеничные средства ТС, а также вертолеты, предъявляющие минимальные требования к транспортной инфраструктуре. В результате резко увеличивается стоимость добычи сырья, легко уязвимые тундровые и таежные экологические системы получают непосильную перегрузку.
Продолжается интенсивная деградация местных воздушных перевозок, что, помимо отрицательных экономических последствий, имеет значительные негативные социальные результаты. Ухудшается связь населенных пунктов с административными центрами, снижается качество транспортного обслуживания населения, становятся недоступными медицинские услуги и т.д. Свертывание местных авиационных перевозок является одним из факторов, способствующих оттоку населения с территорий, и без того крайне редко населенных.
Местные авиационные перевозки дорогостоящи; морское и речное судоходство возможны в короткий летний период; применение автотранспорта затрудняется, в т.ч., по экологическим причинам, из-за сезонности, и др.
Недостаточные пропускные возможности речного транспорта, отсутствие сети железных дорог и высокая стоимость авиационных перевозок (рентабельны на расстояниях более 500 км) привели к тому, что на долю автомобильного транспорта приходится около 70% грузовых и пассажирских перевозок, из которых почти 60% осуществляется по грунтовым дорогам и автозимникам. Однако в весенне-осенний период оттаявшая тундра, переувлажненные грунты и заболоченная местность становятся практически непроходимыми для автомобильного транспорта всех видов. В это время применяется гусеничная техника, осуществляющая перевозки на направлениях с небольшими или непостоянными по времени грузопотоками (доставка грузов и персонала на буровые, эксплуатация коммуникаций, аварийно-восстановительные и поисково-спасательные работы, перевозка медицинских работников, изыскательских партий и т.п.).
Особенностью Севера является наличие многолетнемерзлых грунтов практически на всей территории. Эти грунты содержат 60…90% подземных льдов в верхнем 20…30-метровом слое. Протаивание льдов под действием естественных и антропогенных факторов приводит к образованию термокарстовых озер, бугров, провалов и передвижению почв.
Одним из самых распространенных антропогенных воздействий на природу российского Севера является нарушение ТС растительного покрова в летний период. По некоторым данным, под воздействием традиционных внедорожных ТС происходит не менее 70% всех антропогенных нарушений почвенно-растительного покрова тундровых биогеоценозов. Несущая способность переувлажненной тундры в [2] оценивалась в 10–15 кПа, что значительно меньше давления гусеничных (40…50 кПа) и особенно колёсных транспортных средств.(200…300 кПа). За несколько суток колея превращается в ручей, который спустя 2…3 года становится термокарстово-эрозионным оврагом. Естественное восстановление разрушенного почвенно-растительного покрова происходит в течение десятков, а возможно и сотен лет. В настоящее время площадь поврежденного покрова российской тундры составляет около 16%. По имеющимся оценкам, затраты на рекультивацию 1 га поврежденного оленьего пастбища составляют 30…40 тыс. руб. в ценах 1990 г. Только в Ямало-Ненецком автономном округе в результате применения транспортной техники, не адаптированной к условиям тундры, утрачено более 1 млн. 200 га пастбищ домашних оленей, а экономический ущерб природе оценивается в 60 млрд. руб. в ценах 1990 г.
Быстрый и эффективный прорыв в совершенствовании транспортного обслуживания Арктики, Сибири и Дальнего Востока может быть достигнут за счет дополнения существующей транспортной системы амфибийными средствами на воздушной подушке АСВП [1].
Главным качеством АСВП, особо важным в природных условиях Арктики, Сибири Дальнего Востока, следует считать минимальную зависимость от условий базирования и эксплуатации, при минимальном воздействии на окружающую среду, сравнительно высокой скорости движения и приемлемой экономичности и безопасности.
Специфические качества АСВП позволяют им выполнять особую роль в транспортной системе северных регионов России, являясь единственным круглогодично доступным видом транспорта. АСВП практически безальтернативны для пассажирских перевозок как вне, так и внутри Арктики, а также для оперативного транспортного обеспечения работ по разведке и добыче полезных ископаемых, реализации ряда государственных функций, в первую очередь в области оказания экстренной помощи, борьбы с чрезвычайными ситуациями.
АСВП, имеющие массу 5…50 т., коммерческую нагрузку 1…20 т., пассажировместимость 10…150 человек и крейсерскую скорость до 150 км/час, могут активно использоваться для решения транспортных задач на реках (преимущества АСВП в этих условиях общеизвестны). Важно, что АСВП могут эксплуатироваться круглогодично, включая межсезонные периоды ледостава и ледохода. Амфибийность позволяет АСВП выходить на пологий берег и преодолевать большие расстояния по слабо пересеченной местности. По имеющимся данным, при частых (каждые 20…50 км) остановках по маршруту следования экономические показатели АСВП могут существенно превосходить показатели самолетов и вертолетов.
Анализ условий эксплуатации позволил сформировать основные требования к наиболее массовым мобильным машинам для приморских районов:
- грузоподъемность базовой машины – не менее 10 т. (предпочтительны приспособленность к размещению стандартного контейнера ISO, а также возможность сквозной погрузки транспортных средств на грузовую платформу с помощью откидных аппарелей);
- способность двигаться по всем видам подстилающих поверхностей со скоростью не менее 40…45 км/ч;
- габаритные размеры, обеспечивающие беспрепятственное движение по рекам низших технических категорий;
- способность уверенно и устойчиво передвигаться над неровными подстилающими поверхностями (с высотой или глубиной неровностей до 1,6…1,8 м, причем коротких или близких по длине к длине аппарата) или над водными поверхностями ( высотой волны до 1,8 м);
- способность создавать такой уровень воздействия на подстилающую поверхность, который исключает ее невосстановимые повреждения;
- способность преодолевать затяжные подъемы крутизной до 15 град., а также устойчиво двигаться по склонам крутизной до 10 град.;
- способность к сохранению управляемости и курсовой устойчивости при ветре со скоростью до 10…15 м/с под всеми курсовыми углами.
Однако, технические решения, лежащие в основе конструкций распространенных в настоящее время СВП, не отвечают требованиям, предъявляемым указанными условиями эксплуатации. Эффективность СВП резко снижается на пересеченной местности, при движении по торосам, на уклонах и косогорах. Они неустойчивы и не имеют необходимой для движения по суше, извилистым узким рекам и в иных случаях стесненной обстановки траекторной управляемости. Наконец, даже на небольших пологих уклонах (более 5о) такие СВП плохо удерживаются на траектории. Потеря подвижности СВП на местности, как правило, происходит из-за потерь воздуха через зазоры между гибким ограждением (ГО) и подстилающей поверхностью. В некоторых СВП этот эффект отчасти удается компенсировать за счет мероприятий, увеличивающих сопротивление движению из-за трения ГО о грунт. С этим, однако, связан повышенный износ ГО и риск его повреждения, а также рост сопротивления движению. Кроме того, классическая конструкция ГО содержит внутренние перегородки, доступ к которым при выключенных нагнетателях и осевшем СВП практически отсутствует, что делает невозможным их ремонт в полевых условиях. Это может вызывать большие трудности при эксплуатации СВП в малонаселенных районах.
Анализ характерных свойств традиционных АСВП показал, что они не полностью подходят для транспортных систем российского Севера.
Движение традиционных АСВП обеспечивается, как правило, с помощью аэродинамического винта [3]. Он позволяет развивать сравнительно высокие скорости (до 100 км/ч) над ровными и пологими опорными поверхностями, в т.ч. над водой, ледяной или снежной равниной. Аэродинамические винты при характерных невысоких скоростях транспортного средства (судна) \(v_v\) относительно скорости отбрасываемого воздуха \(v_a\) имеют невысокую эффективность: отношение к потоку энергии \(\frac{1}{2} A \rho v_a^2\) мощности упора (тяги), связанной с силой отдачи от потока импульса \(\frac{1}{2} v_v A \rho v_a\), сравнительно низкое (\(A\) – характерная площадь сечения потока, \(\rho\) – плотность воздуха). АСВП с воздушным движителем неустойчиво и не имеет траекторной управляемости, необходимой для движения по суше, извилистым узким рекам и в иных случаях стесненной обстановки. Такие АСВП имеют крайне ограниченные возможности движения по заданной траектории даже на сравнительно небольших пологих уклонах (более 5 град).В полном объеме эти трудности можно преодолеть в амфибийном транспортном средстве с гибридным опорно-ходовым комплексом (с частичной разгрузкой контактного движителя при помощи воздушной подушки) [4–11]. Основная масса поддерживается ВП, а нагрузка на контактный движитель регулируется таким образом, чтобы обеспечить уровень тягово-сцепных свойств, необходимый для уверенного маневрирования, преодоления подъемов и удержания машины на курсе при боковом воздействии.
Водомётные движители, иногда применяемые для амфибийного транспорта, также не свободны от недостатков, в т.ч. [12–15]
- Меньший, по сравнению с винтом, КПД, из-за:
- Необходимости перевозки, помимо собственно полезного груза, также и воды, находящейся в трубопроводе (в качестве рабочего тела);
- Потери мощности из-за трения воды в трубопроводах;
- Потери мощности из-за турбулентных завихрений потока воды в каналах водомёта.
- Затруднительность подачи воды сквозь днище судна к насосу, на эффективность которого будет влиять скорость движения судна относительно воды.
- Водозабор работает также как помпа и может затянуть со дна камни, песок, мусор. Это может забить систему охлаждения либо повредить импеллер и водовод.
- Водометный движитель разрушает дно прибрежной полосы
- Высока степень износа пары ротор-статор, так как эксплуатация производится на мелководье.
- Резкое и внезапное снижение КПД и упора при уменьшении скорости.
При движении по воде или заболоченной местности колёсные движители малопригодны; предпочтительными представляются гребные колёса. Гребные колёса с неподвижными или поворотными лопатками используются обычно в качестве движителей судов [16]. Они обеспечивают большой упор при малом заглублении, т.е. применимы на мелководье [17]. При малых скоростях судна \(v_{v} = 10\ldots 20\;\text{км/ч}\) они отличаются высокой эффективностью, определяемой как отношение мощности, связанной с силой от колеса \(\boldsymbol{F}\), к механической мощности на валу,
\[\eta = \frac{\boldsymbol{F}\cdot\boldsymbol{v}_v}{\left| \boldsymbol{M} \cdot \boldsymbol{\omega} \right|},\]
где \(\boldsymbol{M}\) – вращательный момент на валу, \(\boldsymbol{ω}\) − угловая скорость вращения колеса.
Длительное время их использование было ограничено [18], что связано, во-первых, с недостаточной надёжностью поворотных лопаток, особенно при высоких скоростях вращения колеса, во-вторых, с тем, что при повышении скорости судна \(v_v\) до \(20\ldots30\;\text{км/ч}\) эффективность движителя \(\eta\) как с поворотными, так и с неподвижными лопатками обычно существенно снижается. Правда, в настоящее время, по-видимому, в связи с достижением предельных характеристик конкурирующих движителей для тихоходных мелкосидящих судов, отмечается некоторый рост интереса к колесным движителям [19; 20].
Принципиальные ограничения эффективности колёсного движителя с неподвижными лопатками при высоких скоростях в литературе практически не описаны. Поэтому представляет значительный интерес изучение и устранение указанных ограничений с целью создания колёсного движителя, эффективного и на высоких, и на низких скоростях судна.
Наши исследования показали принципиальную возможность получения высоких значений энергетической эффективности гребных колёс не только при малых скоростях (порядка 10 км/ч), но и до 40…45 км/ч [21; 22]. При превышении критической скорости, составляющей обычно \(v_{v}^{*} = 25\ldots 35\;\text{км/ч}\), могут значительно снижаться затраты энергии на взаимодействие с водой.
При повышении скорости судна, встают новые проблемы. Гребные колёса, как правило, имеют большие габаритные размеры [18], что может оказывать воздействие на аэродинамические характеристики судов. Если, для относительно тихоходных судов (\(v_{v} = 10\ldots 20\;\text{км/ч}\)), взаимодействие с воздухом играет второстепенную роль в общем сопротивлении движению, то при повышении скорости судна до \(40\ldots 50\;\text{км/ч}\), аэродинамическое сопротивление выходит на первый план, и его необходимо учитывать при выборе геометрии движителя, как заметной части обтекаемого воздухом судна. Причем, как показано ниже, недостаточно решать только аэродинамическую задачу, т.к. при высоких скоростях может возникать существенное нелинейное взаимодействие воздушной и водной сред.
Воздушная подушка ВП (повышенное давление воздуха, поддерживающее аппарат) создаётся под днищем АСВП в объёме, ограниченном гибким ограждением ГО, с помощью вентиляторов-нагнетателей, приводимых в движение двигательной установкой. Гибкое ограждение классического типа расположено по периметру днища. Часто имеются внутренние перегородки, разделяющие объём воздушной подушки на 3…4 части, что повышает устойчивость АСВП. Такая конструкция ГО, правда, сильно затрудняет ремонт указанных перегородок в полевых условиях, т.к. при неработающих нагнетателях АСВП днищем опирается о землю.
При эксплуатации АСВП на местности потеря подвижности, как правило, происходит из-за снижения давления в ВП в результате потерь воздуха через зазоры между ГО и подстилающей поверхностью. В АСВП с комбинированными двухъярусными ГО, наиболее приспособленными для амфибийного использования, компенсировать падение давления отчасти удается принудительным снижением давления в гибких ресиверах. При этом существенно увеличивается сопротивление движению АСВП в результате трения ГО о грунт, увеличивается износ ГО и возрастает риск его повреждения.
Наличие воздушного зазора по всему периметру и ГО малой жесткости, характерное для большинства АСВП классического типа, приводит к неустойчивому равновесному состоянию АСВП и возникновению продольно-угловых и поперечно-угловых колебаний при движении АСВП.
В значительной степени эти недостатки ГО традиционного типа преодолеваются при применении ГО, составленной из отдельных параллельно работающих конических элементов.
Т.о., решение вышеописанной транспортной проблемы российского Севера с учётом как энергетических, так и экологических требований может быть достигнуто при разработке инновационных АСВП, применяющих целый комплекс новых технических решений.
Новизна и сложность задач разработки таких АСВП предопределили необходимость применения технологии комплексных математических моделей, описывающих в различных условиях применения взаимодействующие подсистемы, в которых рабочие процессы традиционно относятся к различным областям знаний (см. [23; 24]). Такие комплексные математические модели имеют модульную структуру, позволяющую проводить не только интерполяцию и экстраполяцию известных конструкций на нужные масштабы, но также сравнение альтернативных традиционных и инновационных технических решений узлов и агрегатов с точки зрения критериев применения аппаратов в целом.
Созданные в данной работе комплексные математические модели позволяют исследовать в сравнении как традиционные, так и инновационные конструкции АСВП при различных условиях эксплуатации, в т.ч. характерных для Севера и Дальнего Востока, включая аварийные ситуации.
Программное решение
Быстрый рост вычислительной мощности ЭВМ в последние десятилетия делает возможным использование компьютерного математического моделирования для все более сложных объектов. Использование математического моделирования позволяет избежать многократного использования прототипов и, при правильном подходе, позволяет сократить стоимость разработки концептуально новых решений и продуктов.
При моделировании сложных технических объектов важной оказывается возможность изолированного исследования подсистем, составляющих данный объект. Это связано как с необходимостью верификации построенных математических моделей, отладки построенных программных комплексов, так и с необходимостью решения задач различных дисциплин в различных подсистемах. Изолированное исследование подсистем технически сложного объекта позволяет, с одной стороны, верифицировать и отлаживать более простые системы, и затем идти от простого к сложному, а с другой стороны, упрощает разработку, параллельно ведущуюся различными группами исследователей. Модель объекта, составленную из моделей подсистем, можно представить, как некий комплекс моделей, или комплексную модель. Дополнительным преимуществом использования комплексных моделей является возможность повторного использования уже разработанных моделей подсистем для использования в комплексных моделях других объектов, т.е. использования некой библиотеки моделей при разработке.
При моделировании технически сложных объектов возникают вычислительные задачи большой размерности, для решения которых оказывается необходимо применять различные специализированные математические методы. Для уменьшения размерности задачи могут использоваться также подходы иерархического моделирования и табличного задания процессов с использованием экспериментальных или модельных результатов.
Использование библиотеки моделей накладывает требование возможности быстрой адаптации библиотечных моделей под условия разрабатываемой.
На основе вышесказанного, а также нашего многолетнего опыта разработки комплексных моделей различных объектов (космических энергоустановок [25], гиперзвуковых летательных аппаратов [23; 24], судов на воздушной подушке [7] и др.) можно сформировать следующие требования для программного комплекса, решающего задачу комплексного моделирования:
Автоматическая сборка комплексной модели из моделей подсистем
Возможность использования различных численных методик для решения задач высокой размерности (в т.ч. поддержка пользовательских компонентов-решателей)
Поддержка подходов иерархического моделирования и табличного задания процессов
Возможность быстрой корректировки библиотечных моделей под изменяющиеся требования
С точки зрения удобства использования программного пакета, можно сформулировать несколько дополнительных требований:
Графическое редактирование связей между моделями подсистем
Использование стандартного языка для разработки моделей
Низкая стоимость лицензии на одно рабочее место
Графическое редактирование является наиболее наглядным представлением, что дает более высокую устойчивость к ошибкам. Использование стандартного языка уменьшает порог вхождения и затраты на обучение. Последнее требование продиктовано необходимостью возможности параллельной разработки различными группами исследователей: при высокой стоимости лицензии на рабочее место, необходимы либо крупные капиталовложения для обеспечения каждой группы, либо дополнительные программные и технические средства для обеспечения параллельного или удаленного доступа к программному комплексу.
Часть 1. Программное решение
Анализ существующих решений
На текущий момент на рынке программного обеспечения существует ряд решений для блочного и компонентного моделирования систем. Многие из этих решений на данный момент активно развиваются. Тем не менее, большинство из существующих решений оптимизировано под определенные классы задач, в связи с чем их применение к более широкому кругу проблем оказывается осложнено.
Наиболее известными сейчас являются решения для блочного моделирования, такие как Matlab Simulink[???], VisSim[???], и их открытые аналоги, такие как Scicos[???]. Общей проблемой подобных решений является их ориентированность на разработку моделей для обработки сигналов, в частности электрических и гидравлических цепей. Несмотря на то, что для подобных применений эти решения подходят достаточно хорошо, для реализации более сложных моделей требуются значительные усилия[???].
Другой проблемой этих систем является часто жестко заданный набор решателей дифференциальных уравнений. В случае систем с открытым исходным кодом эта проблема стоит не столь остро, однако, если поставляемые решения не удовлетворяют требования решаемой задачи, добавление пользовательских решателей в открытые системы оказывается сопряжено с большим количеством работы по освоению существующей кодовой базы [???].
Сравнительно новой альтернативой подходу блочного моделирования является компонентное моделирование систем. К программным решениям этого класса относятся, например, EcosimPro[???], ASCEND[???], EMSO[???] и различные реализации стандарта Modelica[???], как открытые, например, OpenModelica[???] и JModelica[???], так и проприетарные, например, Dymola[???], MapleSim[???], AMESim[???] и др.
Все перечисленные решения для компонентного моделирования обладают общей проблемой: адаптация старых исходных кодов моделей на Fortran, C или C++ требует генерации специальным образом сформированной динамической библиотеки (DLL или SO) либо специальным образом сформированного исходного кода (в случае AMESim).
Другой проблемой, вытекающей из предыдущей, является необходимость освоения собственного скриптового языка данной системы. При этом, даже решения на основе Modelica обладают присущими только им особенностями языка, которые необходимо знать для эффективного использования этих решений.
Подключение сторонних решателей и/или интеграторов, как и в случае с решениями для блочного моделирования, также поддерживается не всеми перечисленными программными пакетами. Подробная документация приведена только для ASCEND (в котором на момент написания эта функциональность является экспериментальной) и EMSO.
К недостаткам закрытых решений также можно отнести их высокую стоимость, так, например, Dymola (не продается в России) оценивается в $5000 для полной редакции ($1200 для упрощенной), а дополнительные компоненты, такие, как 3D-визуализация, дополнительно увеличивают стоимость на $1200-1500. AMESim оценивается в $11000, MapleSim – около $7000. Все цены приведены для лицензий на одного пользователя.
Что касается открытых решений, ASCEND, несмотря на длительное присутствие на рынке, на момент написания значительно проигрывает другим программным пакетам по функциональности (которая либо не реализована, либо является экспериментальной). Это позволяет предположить, что разработка ведется крайне медленными темпами. Подобное заключение можно сделать и о “полузакрытом” EMSO, активная разработка которого не ведется с 2010 года, а многие цели, которые планировалось реализовать еще к 2008 году, не реализованы до сих пор. К тому же, по условиям лицензии, основной программный пакет EMSO доступен только для образовательных и некоммерческих применений.
JModelica, несмотря на активную разработку, на момент написания реализует стандарт Modelica только частично[???], поэтому использование может быть дополнительно осложнено.
Более полное сравнение программных продуктов приведено в табл. 1.
Предлагаемое программное решение
Из вышесказанного следует, что использование существующих программных продуктов для создания и анализа комплексных моделей не всегда удобно. В связи с этим, был разработан новый программный пакет, смягчающий многие из перечисленных недостатков.
Автоматическая сборка комплексной модели из моделей подсистем обеспечивается модулем “компилятора”, принимающим на вход файл-описание и исходные коды и создающим двоичный исполняемый файл комплексной модели, который затем можно использовать отдельно от программного комплекса. Модуль “компилятора” написан с использованием C++ и пакета библиотек Boost.
Модульная архитектура позволяет использование пользовательских интеграторов и решателей. Стандартный API требует от модуля решателя только использования соглашений на именование и прототипы функций и использование XML фиксированного формата для управления настройками решателя и модели.
Использование полного С++ в качестве языка описания моделей позволяет легко вставлять в модели таблично задаваемые параметры с использованием любого метода интерполяции.
Адаптация “старых” моделей как правило сводится к написанию простого “адаптера”, описывающего входы и выходы, и небольшой модификации исходной модели для работы с “адаптером”.
Библиотечные модели целиком копируются в проект, поэтому их изменение в рамках проекта не требует дополнительных действий. Возможна модификация моделей на этапе связывания в комплексную модель.
Инструмент графического редактирования связей между моделями подсистем написан на С++ с использованием графических библиотек Qt.
Все основные инструменты программного пакета написаны на C++ с использованием кроссплатформенных библиотек, что позволяет легко переносить программный пакет на любую платформу с поддержкой этих библиотек, в частности, на Linux, Windows и Mac OSX.
Структура комплексной модели
Математическую модель можно представить, как некую систему уравнений. Система уравнений характеризуется, в свою очередь, переменными, значения которых могут быть постоянны, либо изменяются дискретно или непрерывно, и уравнениями, описывающими связь этих переменных между собой. Для разрешимости задачи математического моделирования необходимо, чтобы система, описывающая данную модель, была замкнутой. Соответственно, если исходная система не замкнута, для введения дополнительных условий оказывается необходимо добавить к исходной еще одну или несколько систем уравнений, описывающих поведение неопределенных в исходной системе переменных. Рассуждая таким образом, можно предложить следующую схему представления моделей подсистем: моделью подсистемы (“простой” моделью) является некоторая система уравнений, имеющая N неопределенных переменных, где N≥0. Совокупность простых моделей можно считать комплексной моделью, причем комплексная модель так же может быть незамкнутой. Окончательно, комплексная модель, пригодная для моделирования, может представлять из себя такую совокупность простых и комплексных моделей, в которой все переменные определены. Переменные, определенные в рамках данной модели, мы будем называть “выходными параметрами”. Переменные, не определенные в рамках данной модели, будем называть “входными параметрами”.
Для описания комплексной модели используется иерархическое дерево: простые модели, описываемые при помощи исходного кода на языке C++ и файла XML с описанием входных и выходных параметров, являются “листьями” этого дерева. “Листья” объединяются в ветви, сами представляющие из себя комплексные модели. Комплексные модели должны дополнительно описывать связи параметров между входящими в них моделями. Наконец, “корнем” дерева является комплексная модель, состоящая из простых и комплексных моделей, в которой все входные параметры определены. Все дерево далее будем называть “проектом”.
В качестве формата файлов проекта выбраны zip-файлы со сжатием deflate, содержащие исходные коды входящих в проект моделей и XML-файл описания, содержащий информацию о входных и выходных параметрах моделей (в т.ч. название, описание, размерность, и т.п.), а также о связях между параметрами и исходном коде. Кроме того, отдельные модели при необходимости сохраняются в аналогичных по структуре zip-файлах и могут быть впоследствии загружены в другой проект.
Модуль “компилятора”
Модуль компилятора преобразует файлы проекта в бинарные исполняемые файлы модели, пригодные для расчетов. Этот процесс происходит в несколько этапов:
Строится граф зависимостей всех параметров модели
Проверяется наличие циклических зависимостей
Исходные коды моделей переписываются в вид, пригодный для использования с модулями решателей
Определяется порядок расчета параметров комплексной модели на основе топологической сортировки
Генерируется функция состояния системы, пригодная для использования с модулями решателей
Полученные коды компилируются и линкуются с решателем при помощи внешнего компилятора С++
Генерируется файл настроек
Граф зависимостей параметров строится на основе синтаксического анализа исходных кодов моделей и связей, указанных в XML-описании проекта. Для проведения синтаксического анализа используются регулярные выражения (библиотека Boost Xpressive).
Поиск циклических зависимостей и топологическая сортировка производятся стандартными алгоритмами.
На третьем этапе все параметры линеаризуются, т.е. представляются в виде массива скаляров, и соответствующие именованные параметры моделей заменяются на внутреннее представление. Кроме этого, во избежание конфликта имен функций, функции моделей переименовываются уникальным образом (добавлением префикса, характеризующего положение модели в иерархии проекта). Входные и выходные параметры, связанные равенством, используют одну ячейку памяти, однако с разным спецификатором доступа: изменение входных параметров запрещено.
Функция состояния системы для случая моделей, описываемых системами ОДУ, возвращает правую часть задачи Коши. Для случая систем ДАУ или алгебраических уравнений – вектор остаточных членов системы.
Файл настроек представляет из себя файл XML, содержащий информацию о начальных значениях параметров, задаваемых дифференциальными уравнениями, значениях параметров, обозначенных как постоянные, и настройках модуля решателя.
Инструмент графического редактирования связей
Инструмент графического редактирования связей предназначен для связывания отдельных “простых” моделей в комплексную. Модель графически представляется в виде прямоугольника с выходящими из его ребер линиями с квадратом на конце (далее “блок”), отражающими входные и выходные параметры модели (далее “коннекторы”). При этом, “входные” коннекторы (для входных параметров) расположены на правой грани, “интегрируемые” – на верхней, постоянные – на нижней и “выходные” – на правой (рис. 1, 2)
Методом “drag&drop” возможно связывание всех прочих коннекторов с входными. Для упрощения визуального восприятия, коннекторы автоматически кодируются цветом. Цвета связующей линии и входного коннектора соответствуют цвету связанного выходного коннектора. Возможно связывание одного выходного коннектора с несколькими входными, но не наоборот.
Также возможно создание блоков комплексных моделей, включающих в себя несколько “простых” или других комплексных моделей, как полностью определенных, так и частично. При этом неопределенные в рамках такого блока параметры должны быть “экспортированы” (экспорт реализуется пунктом контекстного меню коннектора). На блоке комплексной модели отображаются только коннекторы “экспортированных” параметров. Блок комплексной модели можно “развернуть” двойным кликом на нем.
Любой блок может быть сохранен в виде файла модели. Так же любой ранее сохраненный блок возможно загрузить в новую модель.
Кроме того, инструмент графического редактирования связей включает в себя возможности для редактирования исходного кода моделей, добавления или удаления параметров и возможности создания новых моделей в процессе работы.
Модуль решателя
Модуль решателя представляет из себя статическую библиотеку со строго определенным API. Строго говоря, API определяет всего одну функцию solve с одним параметром – экземпляром вспомогательного класса, предоставляющим информацию о времени счета, времени остановки, настройках решателя, а также вспомогательные функции, реализующие инициализацию, вывод и расчет правых частей задачи Коши.
На текущий момент реализованы следующие решатели:
Решатель DOPRI5[???] (адаптирован из старого кода на языке FORTRAN)
Решатель RADAU5[???] (адаптирован из старого кода на языке FORTRAN)
Решатель SUNDIALS CVODE[26] (написан интерфейс, “стыкующий” библиотеки SUNDIALS с API решателя)
Инструмент анализа решения
Инструмент анализа решения позволяет изменять начальные условия и постоянные без повторной сборки модели. Кроме того, графически отображает решение, позволяет сохранять и конвертировать файл решения в различные форматы (на текущий момент ascii-таблица и tecplot).
Формат решения предполагает текстовое описание, которое также вводится из интерфейса данного инструмента.
В процессе решения, графики периодически обновляются (рис. 3). Так же отображается общий прогресс решения.

Возможен многопараметрический анализ, реализуемый многократным расчетом модели (рис. 4)

Пример использования
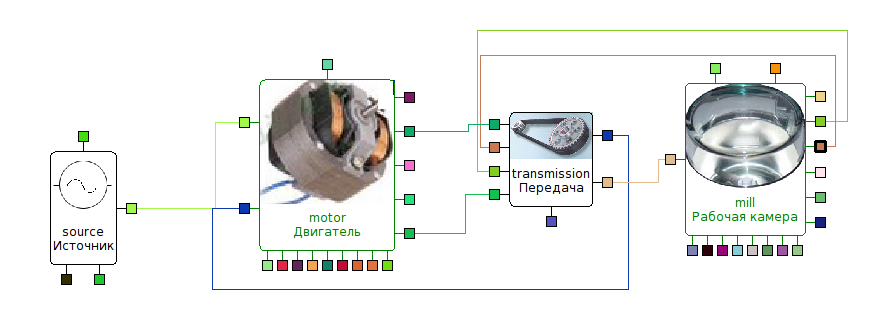
Рассматривается пример использования предлагаемого программного средства для моделирования технически сложных объектов на примере мельницы для измельчения твердых органических материалов. С одной стороны, подобное устройство годится как пример системы, принцип действия которой знаком из бытовой техники, с другой стороны, его моделирование и оптимизация потребовались, в частности, для решения задачи экономически эффективного получения микронных порошков органического сырья, критически важной для масштабной программы получения биотоплива.
Структурная схема комплексной модели показана на рис. 1. Комплексная модель мельницы состоит из блоков:
Модель асинхронного однофазного электрического двигателя
Модель ременной передачи
Модель источника синусообразного тока
Модель рабочей камеры
Модель электрического двигателя разработана в нашей работе [25] на основе [27; 28]. В модели учтены эффекты влияния ширины зазора, взаимовлияние катушек ротора и статора, индуктивности рассеяния катушек, описывается динамика раскрутки и торможения ротора, динамические эффекты на стартовом конденсаторе. Оценивается стоимость двигателя (пропорционально объему материалов, требуемых для его изготовления, что верно при массовом производстве).
Модель помола построена на основе предположения, что обмен импульсоммежду частицами эффективен, т.е. что частицы движутся с минимальнымискоростями относительно друг друга. Тогда скорость частиц \(v\) направленатангенциально, причем её модуль пропорционален радиальному размеру \(r\):
\[v = \omega r.\]
Частота вращения ω определяется уравнением баланса моментов для вращения [29].
\[J \frac{\partial\omega}{\partial t} = M_i - M_w.\]
Здесь \(J\) − момент инерции, \(t\) − время, \(M_i\) − вращательный момент отударного взаимодействия частиц с ножом, \(M_w\) − вращательный момент оттрения частиц о стенку. Для цилиндрической засыпки
\[J = \int_0^R\rho r^2 dV = \int_0^R \rho r^2 h 2\pi r dr = \frac{1}{2}\pi\rho h R^4,\]
здесь \(V\)− объём, \(h\) − высота, \(\rho\) − плотность засыпки, \(\rho\) = \(C_\rho \rho_0\),\(C_\rho\) − объёмная доля твердого материала, для сферических частиц \(C_\rho=\pi/6\), \(\rho_0\) − плотность твердого материала, \(R\) − радиальный размеркамеры. При трении частиц о стенку тормозящий момент
\[M_w = C_w p_w (2\pi R h) R,\]
здесь \(C_w\) − коэффициент трения, \(p_w\) − давление на стенку, для цилиндрической засыпки
\[p_w = \int_0^R a\rho dr = \int_0^R r\omega^2 \rho dr = R^2 \omega^2 \rho.\]
Здесь \(a\) − ускорение. Вращательный момент от ударного взаимодействиячастиц с двумя ножами
\[ M_i = 2 R_k \nu_k (C_k+1) 2 m (v_k - v_m) = \] \[ 2 R_k (C_k+1) 2\rho h_k \delta_k (R_k\Omega - R_k\omega)^2 = \] \[ 4(C_k+1) R_k^3 \rho h_k \delta_k (\Omega-\omega)^2,\]
здесь \(R_k\) − радиальная координата рабочей поверхности ножа, \(h_k\) −её высота, \(\delta_k\) − толщина, \(m\) − масса частицы, \(\nu_k\) − частота соударений, \(v_k\) − скорость ножа, \(v_m\) − скорость частицы досоударения, \(\Omega\) − частота вращения ножа, \(C_k\) − коэффициент упругости удара, \(C_k = 1\) для абсолютно упругого и \(C_k = 0\) для абсолютно неупругого удара.
Помол при высокоскоростном ударе рассчитывался из уравнения [???]
\[\frac{\partial N_p(t)}{\partial t} = N_{p0} K \frac{v_{rel}^2}{\sqrt{x_p}}\]
здесь \(v_{rel}\) − относительная скорость столкновения частицы и ножа, \(t\) − время, \(N_p(t)\) − текущее, \(N_{p0}\) − начальное число частиц, \(x_p\) − текущий средний характерный размер частиц, связанный с \(N(t)\), \(K\) − коэффициент, определяемый механическими свойствами обрабатываемого материала.
Каждый из блоков разрабатывался и тестировался отдельно. Полные исходные коды модели составляют 170 строк. Исходные коды, сгенерированные компилятором, составляют 809 строк.
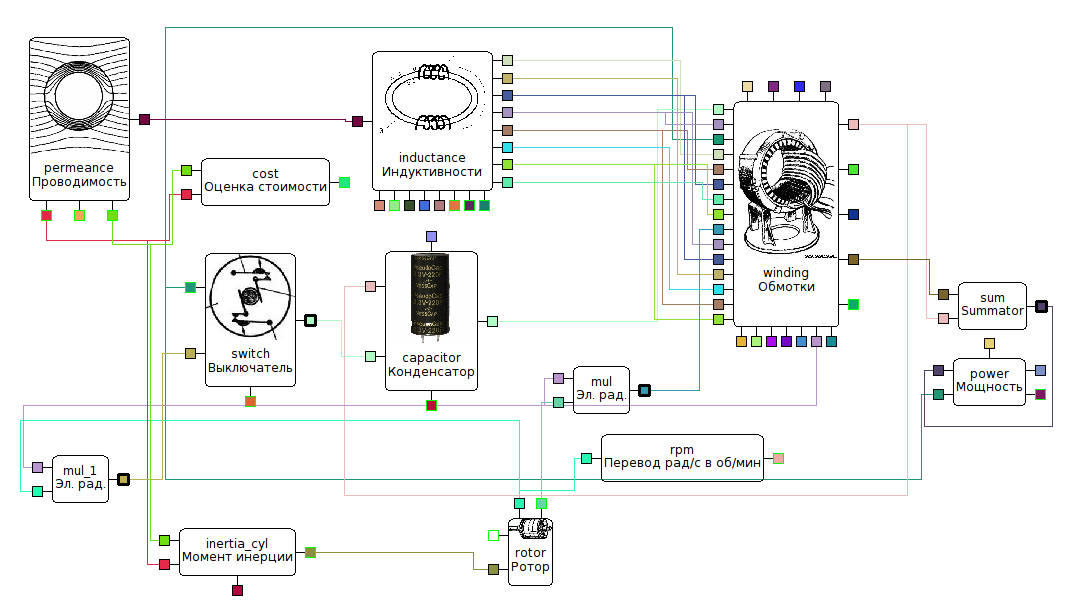
На рис. 2 показана структурная схема комплексной модели электрического двигателя. Модель двигателя можно изолированно использовать, например, для анализа раскрутки ротора в режиме холостого хода. Так, например, при увеличении момента инерции ротора (за счет увеличения радиуса), время раскрутки увеличивается (рис. 3).
При использовании модели электродвигателя в составе модели мельницы отдельные модели автоматически объединяются в общий комплекс. С помощью этого комплекса можно проводить анализ и оптимизацию различных характерных параметров конструкции и режимов, например, в терминах стоимость-производительность. Под производительностью понимается масса измельченного материала, отнесенная ко времени измельчения.
В качестве примера, рассмотрим задачу оптимизации соотношения производительность/стоимость по параметру размера рабочей камеры. Проводится несколько серий расчетов работы мельницы при пропорциональном изменении размеров элементов двигателя. Для каждого набора параметров определяется время достижения необходимого размера частиц (300 мкм). По заданной массе материала определяется производительность. По геометрическим параметрам определяется стоимость. Строится график производительности от стоимости для различных размеров рабочей камеры (рис. 4).
С помощью комплексной модели данного технически сложного объекта продемонстрирована принципиальная возможность использования ее на стадии эскизного проектирования мельницы с целью повышения качества проектирования и снижения издержек на разработку. При этом моделируются аспекты различных рабочих процессов, преодолеваются трудности, связанные с различными пространственными и временными масштабами рабочих процессов в различных подсистемах. Продемонстрирована принципиальная возможность проведения многопараметрического анализа на этапе эскизного проектирования. Показано значительное уменьшение объема необходимого исходного кода (по крайней мере, в 4 раза).
| Simulink | VisSim | Scicos | EcosimPro | ASCEND | EMSO | OpenModelica | JModelica | Dymola | SM1 | MapleSim | AmeSim | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | + | + | + | + | + | + | + | - | + | + | + | + |
| 2 | - | + | * | - | + | + | * | * | - | - | - | - |
| 3 | - | - | * | - | + | + | * | * | - | - | - | - |
| 4 | † | † | † | † | † | † | † | † | † | + | + | + |
| 5 | † | † | † | + | + | + | † | - | + | † | † | + |
| 6 | - | - | - | - | - | - | ‡ | ‡ | ‡ | ‡ | ‡ | + |
| 7 | - | - | - | + | + | + | + | + | + | + | + | + |
| 8 | + | + | + | + | - | + | + | - | + | + | + | + |
| 9 | W,L,M | W | W,L,M | W | W,L | W,L | W,L,M | W,L,M | W,L | W,M | W,L,M | W,L |
| 10 | $5000 | $3840 | Беспл. | $1500-2500 | Беспл. | Некомм. | Беспл. | Беспл. | $5000 | $2450 | $7000 | $11000 |
1. Автоматическая сборка комплексной модели из моделей подсистем. 2. Пользовательские решатели. 3. Пользовательские интеграторы. 4. Табличное задание процессов/параметров .5. Сравнительно легкая адаптация “старых” моделей на компилируемых языках (Fortran, C, etc). 6. Использование стандартного языка для разработки моделей. 7. Быстрая корректировка библиотечных моделей. 8. Графическое редактирование связей между моделями подсистем. 9. Поддерживаемые ОС (W – Windows, L – Linux, M – Mac OSX). 10. Примерная стоимость лицензии на рабочее место
* – функция теоретически доступна, но не поддерживается. Требуется редактирование исходного кода или дополнительные технические приемы.
† – функция, реализуемая посредством сложных манипуляций другими возможностями программы
‡ – использование узко специфичного языка Modelica
Часть 2. Моделирование СВП
Гибкое ограждение классического типа
Математическая модель гибкого ограждения классического типа основана на балансовых и полуэмпирических соотношениях.
ГО классического типа содержит набор (несколько десятков) вертикальных элементов, независимо меняющих форму и угол наклона. Для каждого такого элемента рассчитывается истечение воздуха через щель между ГО и неровной поверхностью. В случае податливости поверхности под ГО (вода, болото и т.п.), вносятся эмпирические поправочные коэффициенты [3]. Объем ГО физически разделен на большие секции (обычно 4…6). В силу дозвукового течения, давление в объеме каждой секции считается одинаковым.
Истечение через щель считается пропорциональным площади зазора под элементом и квадратному корню удвоенного избыточного давления в подушке, отнесенного к плотности воздуха. Так же вводится эмпирический поправочный коэффициент, рассчитываемый в общем случае как \(\mu_i=E\left({\theta,\tau/h,\tau/b}\right)\mu_0\left({\theta}\right)\), где \(E\) – коэффициент, связанный с податливостью подстилающей поверхности и геометрией навесных элементов, \(\mu_0\) – коэффициент расхода воздуха для ГО в виде сплошной полосы над твердым экраном, \(\theta\) – угол наклона навесных элементов или ГО к горизонту, \(\tau\) – ширина щели под ГО, \(b\) – ширина навесных элементов, \(h\) – глубина впадины под ГО, образованной податливой поверхностью. Для жесткого экрана \(E\left({\theta,\tau/h,\tau/b}\right) = 1\).
Подъемная сила воздушной подушки считается как произведение избыточного давления в секции на площадь секции в горизонтальной плоскости. Расчет производится для каждой секции отдельно, затем результирующие векторы сил и моментов сил складываются для получения результирующего крутящего момента и подъемной силы.
В объеме под ГО изменение давления рассчитывается решением следующего дифференциального уравнения для каждой секции [30]:
\[\frac{\partial P}{\partial t}=\frac{c^{2}}{V}(G_{c}- \sum_{i=0} ^{N-1} Q_{i}\rho_{a})\]
Здесь \(c\) – скорость звука в воздухе, \(P\) – давление в секции подушки, \(V\) – объем секции, \(G_c\) – массовый расход на выходе нагнетателя, \(Q_i\) – объемный расход в \(i\)-том элементе (всего \(N\) элементов), \(\rho_a\) – плотность воздуха. В рассматриваемом варианте подушка снабжена четырьмя нагнетателями, по одному на каждую секцию.
Расход нагнетателя связан с давлениями на выходе из нагнетателя и в объеме подушки и геометрией объема подушки [30] следующим дифференциальным уравнением:
\[\frac{\partial G_{c}}{\partial t}=\frac{A}{L}\left(p_{c}-P\right)\]
Здесь \(G_c\) – массовый расход на выходе нагнетателя, \(A\) – характерная ширина потока воздуха, \(L\) – характерная длина потока воздуха, \(p_c\) – давление на выходе из нагнетателя, \(P\) – давление в секции подушки.
Сопротивление движению
Сопротивление движению судна на воздушной подушке определяется как сумма следующих аэродинамических и гидродинамических эффектов [31].
Импульсное сопротивление связано с ускорением поступающего в нагнетатель воздуха до скорости движения судна. Оно пропорционально массовому расходу через нагнетатели и скорости набегающего на судно воздушного потока.
Профильное сопротивление – это сопротивление, обусловленное аэродинамическим сопротивлением корпуса, и рассчитывается по стандартным формулам для турбулентного обтекания исходя из формы корпуса [32].
Сопротивление струй вызвано истечением воздуха из-под воздушной подушки с учетом закона сохранения импульса:
\[\boldsymbol{R}_{str}=\rho_{a}\sum_{i=0}^{N-1}\frac{Q_{i}^{2}}{\tau_{i}L_{i}}\boldsymbol{n}_i\]
Здесь \(\rho_a\) – плотность воздуха, \(Q_i\) – объемный расход воздуха из \(i\)-го элемента, \(\tau_i\) – ширина зазора под элементом, \(L_i\) – длина нижней кромки данного элемента, \(\boldsymbol{n}_i\) – нормаль к огибающей ГО в середине элемента.
Волновое сопротивление связано с работой на образование впадины в воде в пространстве под воздушной подушкой:
\[ R_{wave} = \kappa_{w}^{1}\frac{G_{L} M g}{\alpha_{\Pi}} \]
\[ \alpha_{\Pi} = \frac{S}{L B} \]
\[ G_{L} = \frac{P_{avg}}{\rho_{w} g L} \]
Здесь \(\alpha_\pi\) – коэффициент заполнения площади подушки, \(G_L\) – продольный коэффициент загрузки , \(P_{avg}\) – среднее давление в подушке, \(\rho_w\) – плотность воды, \(g\) – ускорение свободного падения, \(L\) – длина подушки, \(B\) – ширина подушки, \(S\) – площадь подушки, \(M\) – масса судна, \(\kappa_w^1\) – эмпирический коэффициент, задаваемый графически [33].
Другие составляющие гидродинамического сопротивления (от брызг, касания ГО воды и др.) принято обозначать как остаточное сопротивление \(R_{res}\) [34]:
\[ R_{res} = \frac {c_{\Gamma0} L} {\left({\tau/L}\right)^{0,34}} \sqrt{S} \frac {\rho_{w}v^{2}} {2} + \left\lbrack{ \frac {5,09} {\left({G_{L} \rho_{w} g}\right)^{0,259}} - 1 }\right\rbrack R_{wave} \]
где \(\rho_w\) – плотность воды, \(v\) – скорость судна, \(\tau\) – средняя величина зазора, \(L\) – длина подушки, \(S\) – площадь подушки, \(c_{ГО}=15.4 \cdot 10^{-6}\) , \(G_L\) – продольный коэффициент загрузки, \(g\) – ускорение свободного падения, \(R_{wave}\) – волновое сопротивление.
Нагнетатели
В основе описания рабочих процессов в аксиальном нагнетателе лежит полуэмпирический подход, описанный в [35–39].
Полуэмпирические соотношения основаны на обработке большого массива экспериментальных данных, они в исследованных расчетных режимах даже дают более точные результаты, чем подробные 3D вычисления (погрешности которых связаны с неточностью описания турбулентных течений, технической сложностью разрешения пограничных слоев, численными эффектами и пр.). Однако область применимости таких поправок не охватывает многие нерасчетные режимы. Попытки экстраполяции полуэмпирических соотношений в нерасчетные режимы приводит к большим ошибкам и даже к физически бессмысленным результатам. В результате вблизи расчетных режимов лучший результат дают полуэмпирические поправки, а в нерасчетных режимах лучшие результаты получаются, если эти поправки не учитываются вообще. При этом поправки, полученные ранее на основе вычислений в трехмерных постановках для сильно нагруженных лопаточных машин, оказываются непригодными для нагнетателей АСВП, в которых повышение давления составляет малую долю начального давления. В принципе, для нерасчетных режимов нагнетателей АСВП нужно проводить дополнительные исследования, например, подробное математическое моделирование в трехмерных постановках. Это, однако, выходит за рамки данной работы.
Поэтому при разработке данной модификации математической модели необходимо было как можно точнее из основных принципов описывать рабочие процессы, не выходя за рамки неплохо обоснованного канального приближения. Применено теоретическое описание газодинамических процессов на основе балансовых соотношений [40–42] , отражающих сохранение массы, импульса и энергии. Требования описания многих режимов не позволяют использовать упрощающие предположения, с успехом применяющиеся при проектировании [36; 37].
Здесь и далее скорости в лабораторных координатах обозначены \(c\), скорости во вращающихся координатах, связанных с рабочим колесом – \(w\), скорость вращения колеса в рассматриваемом месте колеса – \(u\), скорость звука – \(a\) или \(v_s\), индексом \(u\) или \(\theta\) обозначены проекции скоростей на направление азимутального вращательного движения в данном месте колеса, индексом \(a\) – проекции скоростей на направление оси симметрии, индексом \(r\) – радиальные составляющие скоростей. Индексом \(1\) отмечены параметры на входе в подвижные лопатки, \(2\) – на выходе из подвижных рабочих лопаток, \(3\) – в выходном патрубке нагнетателя (после успокоения потока).
Рассмотрим описание физической и математической постановки для модуля, предназначенного для расчета процессов в нагнетателе.
Полагалось, что на входе в нагнетатель известны давление \(p_1\), температура газа \(T_1\) и массовый расход \(G\). Скорость потока на входе параллельна оси вращения колеса. По известным давлению и температуре на входе в подвижные лопатки (состояние 1) находятся значения остальных параметров: плотности, скорости потока, скорости звука.
\[\rho_1 = \frac{m_{mol} p_1}{k_B T_1}\]
\[c_{1a} = \frac{G}{\rho_1 F_0}\]
\[c_1 = c_{1a}\]
\[c_{1\theta} = 0\]
\[v_{s1} = \sqrt{\frac{k k_B T_1}{m_{mol}}}\]
\[M_1 = \frac{c_1}{v_{s1}}\]
где \(F_0\) – площадь сечения каналов на входе в лопатки, перпендикулярного оси вращения.
По найденным характеристикам потока, набегающего на рабочее колесо, определяются модуль и направление относительной скорости \(w_1\), число Маха набегающего потока во вращающихся координатах рабочего колеса \(M_{w1}\), угол входа потока в каналы рабочего колеса \(\beta_{11}\), температура торможения \(T_{w1}^*\):
\[u = \omega r_0\]
\[w_{1\theta} = c_{1\theta} - u\]
\[w_{1a} = c_{1a}\]
\[\beta_{11} = \arctan\left(\frac{w_{1a}}{w_{1\theta}}\right)\]
\[w_1 = \sqrt{w_{1a}^2 + w_{1\theta}^2}\]
\[M_{w1} = \frac{w_{1t}}{v_{s1}}\]
\[T_{w1}^* = T_1 + \frac{w_1^2}{2C_p}\]
где \(\omega\) – угловая скорость, \(C_p\) – удельная теплоемкость газа.
Находится эффективное критическое сечение канала и по нему – число Маха на выходе и остальные параметры в сечении “2” как в координатах колеса, так и в лабораторных координатах. При этом возникает необходимость решения трансцендентного уравнения:
\[F_{21} = F_0 \sin \beta_{11}\]
\[F_{2cr} = F_{21} M_{w1} \left({\frac{ k + 1 }{ 2 + M_{w1}^2(k-1) }}\right)^{\frac{k+1}{2\left({k-1}\right)}} \]
Оно решалось численно, результаты аппроксимировались и применялись при дальнейших расчетах.
\[M_{w2} = M'\frac{F_2}{F_{2cr}}\]
\[c_{cr} = \sqrt{\frac{w_1^2 (k-1)+2 v_{s1}^2}{k+1}}\]
\[T_{cr} = \frac{m_{mol} c_{cr}^2}{k k_B}\]
\[T_2 = T_{cr} \frac{2+\left({k-1}\right)}{2+\left({k-1}\right) M_{w2}^2}\]
\[a_2 = \frac{k k_B T_2}{m_{mol}}\]
\[w_2 = M_{w2} a_2\]
\[w_{2a} = w_2 \sin \alpha_2\]
\[w_{2\theta} = w_2 \cos \alpha_2\]
\[\rho_2 = \frac{G}{w_{2a} F_0}\]
\[p_2 = \frac{\rho_2}{m_{mol} k_B T_2}\]
\[c_{2a} = w_{2a}\]
\[c_{2\theta} = w_{2\theta} − u\]
\[c_2 = \sqrt{c_{2a}^2 + c_{2\theta}^2}\]
\[M_2 = \frac{c_2}{a_2}\]
где \(k_B\) – постоянная Больцмана, \(m_{mol}\) – масса молекулы газа, индекс \(cr\) относится к параметрам в эффективном критическом сечении.
По найденным параметрам в сечении “2” находится давление торможения в предположении, что восстанавливается осевая составляющая скорости, а азимутальная диссипирует:
\[p_{3i} = p_2 + \frac{\rho_2 c_{2a}^2}{2}\]
Потери на входе в подвижные лопатки учитываются с помощью фактора, равного по определению
\[ Y = \frac{p^*_{in} - p^*_{out}}{p^*_{out} - p_{out}}\]
где \(p^*_{in}\), \(p^*_{out}\) – полное давление на входе и выходе, \(p_{out}\) – статическое давление на выходе лопаток.
Значение \(Y_P\) находится из соотношения
\[ Y_P = \mu \chi \left({ Y_{Pr} + \left({ \frac{\alpha_{bin}}{\alpha_{bout}} }\right)^2 \left({Y_{Pi} - Y_{Pr}}\right) }\right) \left({ \frac{5t}{C} }\right)^\frac{\alpha_{bin}}{\alpha_{bout}} + Y_S \]
где значения \(Y_{Pr}\) и \(Y_{Pi}\) снимаются с графиков [43] в зависимости от угла лопатки на выходе \(\alpha_{bout}\) и от отношения шага между лопатками \(s\) к длине лопатки \(C\); здесь \(\alpha_{bin}\) – угол лопатки на входе потока, \(t\) – толщина лопатки, обычно составляющая \(t=(0,15..0,25) C\).
Влияние вязкости учитывается фактором \(\chi\), который зависит от числа Рейнольдса \(Re = w_2 \frac{C}{\nu}\):
при \(Re < 2 \cdot 10^5\), \(\chi = \left({\frac{1}{2} Re \cdot 10^{-5}}\right)^{-0,4}\)
при \(2\cdot 10^5 \leq Re \leq 10^6\), \(\chi = 1\)
при \(Re > 10^6\), \(\chi = \left({Re \cdot 10^{-6}}\right)^{−0,2}\)
Фактор \(\mu\) применяется для учета вторичных вихрей
\[\mu = 1 - \frac{Z_{TE}}{h}\]
\[Z_{TE} = \left(\frac{0,1 F_\theta^{0,79}}{\sqrt{C_R}\left(\frac{h}{C}\right)^{0,55}}+32,7 \frac{\delta^*}{h}\right)h\]
Здесь \(h\) – ширина лопатки в радиальном направлении, \(\delta^*\) – толщина погранслоя, она составляет \((0,008\ldots 0,06) h\), фактор
\[F_\theta = \frac{2s}{C_x}(\tan \alpha_{in}+\tan \alpha_{bout})\cos^2 \alpha_m\]
\[\alpha_m = \frac{\alpha_{bin} + \alpha_{bout}}{2}\]
здесь \(\alpha_{in}\) – угол входа потока, \(C_x\) – длина проекции лопатки на ось.
Учет вклада вторичных потерь:
при \(0\leq x''\leq 0,3\)
\[Y_S = Y_{S0}\left(\exp(0,9 x'')+13x''^2+400x''^4\right)\]
при \(-0,4 \leq x'' \leq 0\)
\[Y_S =Y_{S0} \exp(0,9 x'')\]
\[x'' = \frac{\alpha_{in}-\alpha_{bin}} {\pi-(\alpha_{bin}+\alpha_{bout})} \left(\frac{\cos \alpha_{bin}}{\cos \alpha_{bout}}\right)^{-1,5} \left(\frac{d_{in}}{C}\right)^{-0,3} \]
Учет потерь из-за нерасчетного угла входа проводится с помощью полуэмпирического соотношения [44] для связанного с этим изменения \(\Delta \phi_P^2\) квадрата отношения \(\phi = {c_2}/{c_{2\tau}}\) (\(c_{2\tau}\) – скорость без учета этого вида потерь):
при \(x \geq 0\)
\[ \begin{aligned} \Delta \phi_P^2 & = 3,711\cdot10^{-7} x^8 - 5,318\cdot10^{-6} x^7 \\ & + 1,106\cdot10^{-5} x^6 + 9,017\cdot10^{-5} x^5 \\ & - 1,542\cdot10^{-4} x^4 - 2,506\cdot10^{-4} x^3 \\ & + 1,327\cdot10^{-3} x^2 - 6,149\cdot10^{-5} x \end{aligned} \]
при \(x < 0\)
\[\Delta \phi_P^2 = 1,358 \cdot 10^{-4} x - 8,720\cdot10^{-4}x \]
\[ x = \left(\frac{d_{in}}{s}\right)^{−0,05} \left(\arccos\frac{C_x}{C}+\alpha_{bin}\right)^{−0,2} \left(\frac{\cos \alpha_{bin}}{\cos \alpha_{bout}}\right)^{−1,4} (\alpha_{in}−\alpha^*_{in}) \]
здесь \(\alpha^*_{in} \approx a_{bin}\) – расчетный угол входа потока, \(d_{in}\) – диаметр закругления лопатки на входе.
Описанная комплексная математическая модель должна модифицироваться в ходе разработки при уточнении и принятии новых технических решений; так, может производиться пересчет в подробных 3D постановках с учетом изменения параметров конструкции, режимов и др.
Винтовые движители
Методика расчета фактически разработана на основе классической теории винта [???; 45–53]. Эта теория часто дает более надежные данные, чем математическое моделирование (в т.ч. в трехмерных постановках на основе методов низкого порядка точности при числе расчетных ячеек порядка миллиона), поэтому она не теряет актуальность до сих пор [54].
Для определения возмущения воздушной среды под действием винта необходимо рассчитать дополнительную скорость потока, производимую вихревым следом (индуктивную скорость). Она имеет три составляющие – тангенциальную, осевую и радиальную; при построении вихревого следа обычно пренебрегают радиальной составляющей. Для учета того, что течение сильно неоднородно в радиальном направлении, течение разбивается на элементы, ограниченные соосными цилиндрическими поверхностями.
В данном случае, в отличие от классического подхода, циркуляция и скорость набегающего на лопатки потока заранее не известны, что существенно меняет алгоритм реализации.
Тангенциальная \(u_1\) и осевая \(v_1\) составляющие индуктивной скорости в плоскости винта представляют собой зависимости от циркуляции:
\[u_1(\Gamma) = \frac{k\Gamma}{4\pi r}\]
\[v_1(\Gamma) = -\frac{V}{2} + \sqrt{ \frac{V^2}{4} + u_1 (\omega r - u_1) + 2 \int_r^R \frac{u_1^2}{r^3} dr }\]
Затем находится скорость набегающего потока
\[W_1(\Gamma) = \sqrt{ \left({\omega r - u_1(\Gamma)}\right)^2 + \left({V+v_1(\Gamma)}\right)^2 }, \]
рассчитывается циркуляция
\[\Gamma = \frac{1}{2} b C_y W_1(\Gamma)\]
Полученное уравнение решается методом бисекции относительно \(\Gamma\). Расчет начинается с концевых сечений винта. Здесь \(k\) – число лопастей, \(r\) – текущий радиус, \(\Gamma\) – циркуляция на данном радиусе, \(V\) – скорость осевой обдувки винта, \(\omega\) – угловая скорость вращения винта, \(R\) – наибольшее значение радиуса винта, \(b\) – длина хорды лопасти. Интеграл под корнем в выражении для \(v_1(\Gamma)\) соответствует центробежным силам, которыми в данном случае можно пренебречь, благодаря наличию кольцевой насадки вокруг винта, т.к. она ограничивает движение в радиальном направлении. По этой же причине не учитываются концевые потери: вихревые линии не уходят в область свободного потока, а кончаются на кольцевой насадке.
За винтом осевая и тангенциальная составляющие скорости в два раза больше, чем в плоскости вихревого диска:
\[u_2=2 u_1\]
\[v_2=2 v_1\]
Для области \(r>R\) индуктивная скорость полагается равной нулю.
Аэродинамические коэффициенты \(C_y\), \(C_x\) определяются профилем винта. Они известны для ряда профилей из подробных экспериментальных данных [55, p. [@lushin1994atlas]]. Эти величины находятся с помощью линейной интерполяции и экстраполяции по табличным данным для профиля. В данном примере взят профиль СибНИА С-11.
Если полагать плотность воздуха постоянной в окрестностях винта и равной \(\rho\), подъемная сила, действующая на элемент лопасти и направленная перпендикулярно скорости набегающего потока, может быть найдена, как \(dR_1 = \rho\Gamma W_1 dr\), а сила профильного сопротивления, направленная вдоль скорости набегающего потока, как \(dR_p=\frac{C_x}{C_y}dR_1\).
Сила тяги \(dT_1\) и сила сопротивления \(dQ_1\) для элемента лопасти могут быть найдены, как проекции суммарной силы \(dR_1+dR_p\) на ось вращения и плоскость вращения соответственно.
Мощность \(dL\), необходимая для вращения элемента лопасти, лежащего на окружности радиуса r, может быть определена из момента силы сопротивления \(dM_{Q1}= −dQ_1 r\):
\[dL=dM_{Q1} \omega\]
Для получения суммарных сил и моментов, действующих на лопасть, и мощности, необходимой для вращения лопасти, производится интегрирование по радиусу.
Нередко винты АСВП располагаются частично в зоне аэродинамической тени от корпуса. Основное воздействие от этого на рабочие процессы связано с тем, что скорость воздуха на входе \(V\) не постоянна по площади винта, а зависит от вертикальной и поперечной координат. Распределение скорости \(V(x,y)\) в первом приближении можно рассчитать отдельно по обтеканию корпуса без учета влияния винтов. Тогда взаимодействие лопасти винта и набегающего потока в данный момент зависит от углового положения лопасти. Для незатененных участков расчет полностью аналогичен приведенному выше, а для затененных – проводится с переменной локальной скоростью \(V(x,y)\), при этом получаются различные значения углов потока относительно лопаток, сил, моментов, выходных скоростей и пр. в зависимости от углового положения лопасти.
В качестве начального приближения можно задать \(V(x,y)\) в виде ступенчатой функции. Тогда можно просчитать по представленной выше методике обтекание лопатки при скоростях, соответствующих значениям скорости на уровнях “ступенек”. При задании аэродинамической тени с помощью \(N\) уровней скорости расчет проводится соответственно \(N\) раз. Эти результаты используются в соответствующих участках заметаемого винтом круга при интегрировании по этому кругу сил, моментов, определении выходных скоростей и пр. В качестве начального варианта выбран двухуровневый вариант.
Описанная методика позволяет рассчитать в базовом приближении все основные характеристики движителя: тягу, приложенную к АСВП, момент сопротивления на валу движителя, в зависимости от управляющих воздействий (поворот лопаток движителя, частота вращения вала движителя) и внешних условий (скорость ветра, скорость АСВП, плотность воздуха).
Рулевой комплекс
При применении движителей на основе контактных или гребных колёс для поворота можно применять различные скорости их вращения с одной и другой стороны от АСВП. В классических конструкциях АСВП для руления нередко применяются поворотные винтовые движители, тогда учёт руления сводится к изменению скорости набегающего воздуха и повороту результирующего момента и силы тяги.
Часто однако в классических конструкциях АСВП за винтом находятся рули, представляющие собой вертикально расположенные крыловидные аэродинамические формы, строго говоря - цилиндры с направляющими – аэродинамическими профилями. Для этого случая разработана описываемая ниже математическая модель.
Для расчета сил и моментов используется система координат: ось \(OZ\) направлена по оси винта, ось \(OY\) – параллельно прямым образующим рулей, ось \(OX\) – так, чтобы система координат была правой. Центр \(O\) находится на оси вращения винта.
Рули находятся в переменном по сечению закрученном потоке воздуха, ускоренного маршевым винтом. Для проведения вычислений каждый из рулей разбивается на элементы горизонтальными плоскостями, причем разные элементы разных рулей находятся в разных условиях обтекания (т.к. скорость и направление потока от винта неоднородны по сечению потока).
Поперечная сила, действующая на элемент руля, аналогичная подъемной силе крыла, равна
\[dR_1 = \frac{1}{2} C_v \rho v^2 b_v dy\]
где \(C_v\) – аэродинамический коэффициент подъемной силы для профиля руля, \(b_v\) – длина хорды руля, \(v\) – локальная скорость набегающего на руль потока.
При нахождении скорости учитывается, что индуктивная скорость в вихревом следе вдвое больше, чем в плоскости вихревого диска.
При определении \(C_v\) учитывается локальный угол атаки, зависящий от направления локальной скорости воздуха, ускоренного винтом, и от угла поворота рулей; для этого для каждого элемента руля решается соответствующая стереометрическая задача.
Поперечная сила направлена перпендикулярно скорости потока и используется для управления направлением движения судна.
При взаимодействии рулей с потоком воздуха возникает паразитная сила сопротивления, направленная вдоль потока и по действию аналогичная уменьшению интегральной тяги. Формула для силы профильного сопротивления \(dR_p\) находится по той же формуле с использованием другого аэродинамического коэффициента для профиля руля, аналогичного \(C_x\) для винта. Она направлена против скорости набегающего потока.
Аэродинамические коэффициенты в принципе определяются так же, как и для винта.
Моменты сил определяются по векторной формуле
\[\mathrm{d}\boldsymbol{M}_{R1} = \boldsymbol{r}\times\mathrm{d}\boldsymbol{R}_1\]
\[\mathrm{d}\boldsymbol{M}_{Rp} = \boldsymbol{r}\times \mathrm{d}\boldsymbol{R}_p\]
Для получения суммарных сил и моментов, действующих на решетку рулей, производится интегрирование по всем рулям, реализованное в виде суммирования по элементам рулей.
Описанная методика позволяет рассчитать в базовом приближении все основные характеристики движителя и рулей − тягу и управляющий момент, приложенные к АСВП, момент сопротивления на валу движителя − в зависимости от управляющих воздействий (поворот лопаток движителя, поворот рулей, частоты вращения вала движителя) и внешних условий (скорость ветра, скорость АСВП, плотность воздуха).
Конический элемент гибкого ограждения
Нам не известны работы по теории конического элемента гибкого ограждения, по которым можно было бы построить математическую модель такого типа ГО. Анализ условий работы такого ГО показал большую сложность многомерной параметризации результатов вычислений, т.е. расчёт динамики геометрии ГО должен проводиться одновременно с расчётом всей АСВП. Более того, анализ известных из литературы методов расчета гибких оболочек показал их непригодность для применения в составе комплексной математической модели – закрытость кодов, невозможность в одном методе учесть сопротивление изгибу и сдвигу, конечное растяжение, возможные жесткие элементы, растяжки, сложность задания геометрии ГО, большое время счета и др. Поэтому нами применялась следующая методика. Это заставило разработать оригинальную численную модель ГО и интегрировать её в комплексную модель АСВП.
Нерастяжимую мнущуюся поверхность представим в виде регулярной сетки, близкой к прямоугольной. В каждом ее узле сосредоточена определенная масса (в общем случае, массы узлов могут различаться). Узлы соединены между собой невесомыми пружинами (ребрами). Искомая коническая поверхность имеет \(N_z+1\) слоев, каждый из которых состоит из \(N_\phi\) узлов. Положение и скорость \((i, j)\)-ого узла определяется векторами \(\boldsymbol{x}_{i,j}\) и \(\boldsymbol{v}_{i,j}\).
Динамика каждого узла оболочки во времени определяется уравнениями движения Ньютона. В данной модели на каждый узел, представляемый материальной точкой, действуют силы тяжести, растяжения/сжатия, сопротивления изгибу, трения, давления и реакции опоры.
Сила тяжести \(\boldsymbol{F}_g\) определяется как \[\boldsymbol{F}_g = \rho S h \boldsymbol{g},\] где \(\rho\) – плотность материала, \(S\) – площадь ячейки, \(h\) – толщина оболочки, \(\boldsymbol{g}\) – вектор ускорения свободного падения.
Сила растяжения/сжатия \[\boldsymbol{F}_t = \sum_j k_t \left({1-\frac{L_j}{d_j}}\right)\boldsymbol{d}_j,\] где суммирование ведется по всем смежным ячейкам (в том числе по диагональным направлениям), \(k_t\) – коэффициент упругости (для диагональных направлений коэффициент упругости считается равным \(0,3 k_t\)), \(\boldsymbol{d}_j\) – вектор, соединяющий текущую ячейку с \(j\)-той ячейкой, \(L_j\) – равновесная длина связи.
Сила реакции опоры \(\boldsymbol{F}_{nr} = k_{nr} l^2 \boldsymbol{n}\), где \(k_{nr}\) – коэффициент жесткости взаимодействия, \(l\) – глубина проминания подстилающей поверхности, \(\boldsymbol{n}\) – единичный вектор нормали к поверхности.
Сила трения о воздух \(\boldsymbol{F}_{fr}^{air} = - k_{fr}^{air} \boldsymbol{v}\), где \(k_{fr}^{air}\) – коэффициент торможения о воздух, \(\boldsymbol{v}\) – скорость узла относительно воздуха.
Сила трения о подстилающую поверхность \[\boldsymbol{F}_{fr} = - k_{fr} F_{nr} \boldsymbol{\tau},\] где \(k_{fr}\) – коэффициент трения о землю, \(\boldsymbol{v}\) – скорость ячейки относительно подстилающей поверхности, \(\boldsymbol{\tau}\)– единичный вектор в направлении проекции скорости на подстилающую поверхность:
\[\boldsymbol{\tau} = \frac{\boldsymbol{v} - \left({\boldsymbol{v} \cdot \boldsymbol{n}}\right)\boldsymbol{n}}{\left|{\boldsymbol{v} - \left({\boldsymbol{v} \cdot \boldsymbol{n}}\right)\boldsymbol{n}}\right|}\]
Сила давления \[\boldsymbol{F} = P S \boldsymbol{n},\] где \(\boldsymbol{n}\) – единичный вектор внешней нормали к поверхности оболочки, \(P\) – избыточное давление под оболочкой, \(S\) – площадь ячейки. Сила сопротивления изгибу на каждом узле вычисляется для вертикального и горизонтального направлений. Изгибающий момент вычисляется по формуле
\[M = (C - C_0) E J,\]
где \(E\) − модуль Юнга, например, для резины \(E \approx 10^7 \text{Па}\); \(J\) − момент инерции сечения в соответствующем направлении. Для плоского сечения \(J = \frac{L h^3}{12}\), где \(h\) − толщина гибкой оболочки, \(L\) − средняя длина двух противолежащих ребер (в горизонтальном или вертикальном направлении), исходящих из данного узла, \(C\) – задаваемая координатами узлов шаблона кривизна поверхности в данной точке (в горизонтальном или вертикальном направлении), \(C_0\) – равновесные значения кривизны, при которых силы не возникают.
В случае близкой к равномерной сетки, \[\left|{C}\right| = \frac{1}{R},\] \[R = \frac{a}{2\sin\alpha},\] \[a = 2 L \sin\frac{\alpha}{2},\] \[\cos\alpha = \frac{\boldsymbol{L}_1 \cdot \boldsymbol{L}_2}{L_1 L_2},\] \[L = \frac{L_1+L_2}{2},\]
где \(R\) – радиус кривизны поверхности, \(\alpha\) – угол между двумя противолежащими ребрами, \(\boldsymbol{L}_{1,2}\) – векторы противолежащих ребер.
Силы рассчитываются для трех узлов следующим образом:
\(\boldsymbol{F}_{1,2} = -\frac{M}{L_{1,2}} \boldsymbol{n}_{1,2}\) – для узлов в конце \(\boldsymbol{L}_{1,2}\) соответственно,
\(\boldsymbol{F} = -(\boldsymbol{F_1}+\boldsymbol{F_2})\) – для среднего узла.
Здесь \(\boldsymbol{n}_{1,2}\) – единичные векторы расчетных нормалей к огибающей окружности радиуса \(R\).
\[ \boldsymbol{n}_{1,2} = \frac {\boldsymbol{L}_{1,2} \times (\boldsymbol{L}_{2,1} \times \boldsymbol{L}_{1,2})} \left|{\boldsymbol{L}_{1,2} \times (\boldsymbol{L}_{2,1} \times \boldsymbol{L}_{1,2})}\right| \]
Для решения полученной системы дифференциальных уравнений используется метод IDA [57].
Из-за большой сложности параметризации и счетной эффективности данная модель непосредственно встраивалась в комплексную модель СВП.
Описанная методика и программа тестировались путём проверки выполнения локальных и интегральных балансовых соотношений для конического элемента ГО и его частей.
Характерные результаты вычислений представлены на рис. 5, 6. При наезде на высокой скорости ГО сминается не так, как при низкой скорости из-за большего влияния инерционности, при этом, в частности, возникают колебания оболочки, по-другому изменяется характерная величина зазора, при сходе с препятствия возникают значительные растягивающие напряжения, особенно при наличии на нём выступов с малым радиусом кривизны. Это может приводить к кратковременной потере давления в воздушной подушке, возникновению разрывов оболочки и пр.
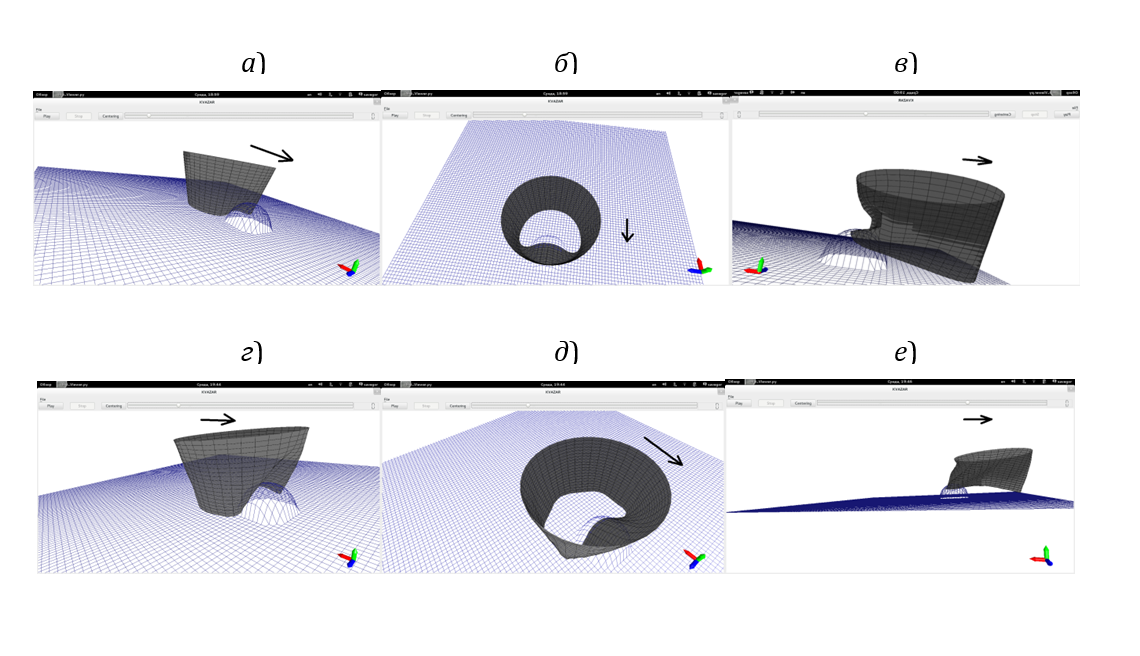

Движители на основе гребных колёс
Модель гребного колеса (рис. 8) строится на основе наших подробных нестационарных гидро-аэродинамических расчетов по методу конечных элементов [21; 22] (рис. 7), применялась полученная там новая форма лопаток и кожуха. По результатам массовых вычислений определялись массивы поправочных коэффициентов в аналитическую модель, аналогично методике, изложенной в [25].

Тормозящий момент на валу колеса представляется как:
\[M_{i} = - (R\omega - v)(\rho \delta L v)R\]
\[\delta = \frac{2 (R \cos\phi + (R-\Delta H) \phi) - (R-\Delta H) \pi}{\pi - 2 \phi}\]
\[\phi = \arcsin\frac{R-\Delta H}{R}\]
где \(\phi\) – угол между поверхностью воды и радиусом в точке входа лопатки в воду, \(v\) – скорость центра колеса относительно поверхности воды в плоскости колеса, \(R\) – радиус, \(\omega\) – угловая скорость вращения, \(\Delta H\) – глубина погружения, \(L\) – ширина колеса, \(\delta\) – средняя по времени глубина погружения лопатки под невозмущенную воду.
Фактический тормозящий момент определяется из данных расчета по МКЭ исходя из соотношений \[M_{r} = \mu_{r} M_{i},\] \[\mu_{r} = \frac{M_{f}}{M_{i}^*},\] где \(M_{f}\) – момент, полученный по МКЭ, \(M_{i}^*\) – идеальный момент \(M_{i}\), рассчитанный для тех же параметров, что и \(M_{f}\).
Тогда сила в направлении движения \[F_x = \eta M_{r} \frac{\omega}{v},\] где \(\eta\) – КПД колеса, определенный из расчета по МКЭ.
Вертикальная составляющая силы колесного движителя определялась из соотношения \[F_y = F_x \frac{F_{yf}}{F_{xf}},\] где \(F_{xf,yf}\) – компоненты \(x,y\) силы, полученные по МКЭ.
\(M_f\), \(\eta\), \(F_{xf,yf}\) – функции скорости вращения колеса \(\omega\), глубины погружения \(\Delta H\), и скорости движения судна \(v\). Значения этих функций определяются интерполяцией результатов, полученных по расчету МКЭ.
Эффективность движителя \(\eta\) определялась как усредненное по периоду между входом лопаток в воду отношение мощности, связанной с силой от колеса \(\boldsymbol{F}\), к механической мощности на валу,
\[\eta = \frac{\boldsymbol{F} \cdot \boldsymbol{v}_{v}}{|\boldsymbol{M} \cdot \boldsymbol{\omega}|},\]
где \(\boldsymbol{M}\) – вращательный момент на валу, \(\boldsymbol{\omega}\) − угловая скорость вращения колеса.
Сила \(\boldsymbol{F}\) вычислялась как интеграл горизонтальных проекций сил давления и поверхностного трения по всей площади поверхности колеса и обтекателя.
Предварительно проводилась расчетная оптимизация формы лопаток и кожуха, позволившая поднять η при скорости судна \(10\ldots45\;\text{км/ч}\) до \(45\ldots 50\;\text{%}\).

Определение геомертрии колеса
В вычислительном эксперименте решалась решалась система уравнений Навье-Стокса для динамики воздуха и воды как среды с переменной плотностью с учётом силы тяжести и с моделью турбулентности SST (вариант k-ω), в приближении изотермичности и малости числа Маха по сравнению с единицей [58]:
\[ \frac {\partial\left({r_{\alpha}\rho_{\alpha}}\right)} {\partial t} + \nabla \cdot \left({ r_{\alpha}\rho_{\alpha}\ \boldsymbol{U} }\right) = 0 \]
\[ \frac {\partial\left({\rho\boldsymbol{U}}\right)} {\partial t} + \left({\boldsymbol{U} \cdot \nabla}\right) \left({\rho\boldsymbol{U}}\right) - \mu_{eff}\Delta\boldsymbol{U} = \left({\rho - \rho_{ref}}\right) \boldsymbol{g} - \nabla p' \]
\[\mu_{eff} = \mu + \mu_{t}\]
\[p' = p + \frac{2}{3} p k\]
\[ \sum_{\alpha} {\nabla \cdot \left({ r_{\alpha} \boldsymbol{U}}\right)} = 0 \]
\[ \rho = \sum_{\alpha} {r_{\alpha}\rho_{\alpha}}, \] \[ \mu = \sum_{\alpha} {r_{\alpha}\mu_{\alpha}} \]
\[ \frac {\partial \left({\rho k}\right)} {\partial t} + \frac {\partial} {\partial x_{j}} \left({\rho U_{j} k}\right) = \frac {\partial} {\partial x_{j}} \left\lbrack{ \left({ \mu + \frac{\mu_{t}}{\sigma_{k3}} }\right) \frac {\partial k} {\partial x_{j}} }\right\rbrack + P_{k} - \beta'\rho k \omega \]
\[ \frac {\partial \left({\rho \omega}\right)} {\partial t} + \frac {\partial} {\partial x_{j}} \left({\rho U_{j} \omega}\right) = \frac {\partial} {\partial x_{j}} \left\lbrack{ \left({ \mu + \frac{\mu_{t}}{\sigma_{\omega 3}} }\right) \frac {\partial\omega} {\partial x_{j}} }\right\rbrack + \left({1 - F_{1}}\right) 2 \rho \frac {1} {\sigma_{\omega 2}\omega} \frac {\partial k} {\partial x_{j}} \frac {\partial\omega} {\partial x_{j}} + a_{3} \frac {\omega} {k} P_{k} - \beta_{3}\rho\omega^{2} \]
\[\mu_{t} = \frac {\rho a_{1}k} {\max\left({a_{1} \omega,SF_{2}}\right)}\]
\[P_{k} = \mu_{t}\left( \frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}} \right)\frac{\partial U_{i}}{\partial x_{j}} - \frac{2}{3}\frac{\partial U_{k}}{\partial x_{k}}\left( 3\mu_{t}\frac{\partial U_{k}}{\partial x_{k}} + \rho k \right)\]
\[F_{1} = \tanh\left({\xi_{1}^{4}}\right)\]
\[ \xi_{1} = \min\left({ \xi_{2}, \frac {4\rho k} {CD_{kw} \sigma_{\omega 2} y^{2}} }\right) \]
\[ CD_{kw} = \max\left({ 2 \rho \frac {1} {\sigma_{\omega 2}\omega} \frac {\partial k}{\partial x_{j}} \frac{\partial\omega}{\partial x_{j}}, 1.0 \times 10^{- 10} }\right) \]
\[ \xi_{2} = \max\left({ \frac {\sqrt{k}} {\beta'\omega y}, \frac{500\mu}{y^{2}\omega\rho} }\right) \]
\[F_{2} = \tanh\left({\xi_{2}^{2}}\right)\]
Здесь \(\alpha = \left\lbrace{water,air}\right\rbrace\) – индекс, соответствующий воде или воздуху, \(r_{\alpha}\) – объемная доля соответствующей фазы, \(\rho\) – плотность, \(\boldsymbol{U}\) – вектор скорости среды, \(t\) – время, \(\mu_{eff}\) – эффективная вязкость среды, \(\mu\) – динамическая вязкость, \(\mu_{t}\) – турбулентная вязкость, \(\rho_{ref}\) – референсная плотность, \(\rho_{ref} = \rho_{air}\), \(\boldsymbol{g}\) – вектор ускорения свободного падения, \(k\) – турбулентная кинетическая энергия, \(\omega\) – удельная скорость диссипации, \(P_{k}\) – возникновение турбулентности от вязких сил, S – инвариантная мера скорости деформации, \(F_{1},F_{2}\) – смешивающие функции, \(y\) – расстояние до ближайшей стенки, \(\beta = 0.09\), \(a_{1} = \frac{5}{9}\), \(\beta_{1} = 0.075\), \(\sigma_{k1} = 2\), \(\sigma_{\omega 1} = 2\), \(a_{2} = 0.44\), \(\beta_{2} = 0.0828\), \(\sigma_{k2} = 1\), \(\sigma_{\omega 2} = 1/0.856\) – модельные коэффициенты, \(\Phi_{3} = F_{1} \Phi_{1} + \left({1 - F_{1}}\right)\Phi_{2}\), где \(\Phi = \left\lbrace{a,\beta,\sigma_{k},\sigma_{\omega}}\right\rbrace\).
Зависимостью параметров от направления вдоль оси вращения пренебрегалось, что хорошо обосновано при характерных условиях, практически устраняющих нежелательные краевые эффекты: при наличии торцевых ограничителей и/или ширине колеса, превышающей ширину лопатки. На одной стороне прямоугольной расчётной области задавались скорости воды и воздуха, равные \(v_v\), постоянное давление воздуха и распределение давления в воде, связанное с гравитацией \(p = \rho_{w} g (H - y)\), где \(H\) – высота уровня воды, \(y\) – вертикальная координата, \(g\) – ускорение свободного падения, \(\rho_{w}\) – плотность воды. На противоположной стороне задавалось свободное истечение с аналогичным распределением давления. На верхней границе задавалось свободное втекание и истечение воздуха \(\nabla \left({\boldsymbol{v}\cdot\boldsymbol{n}}\right) = 0\), \(p = p_{0}\), где \(\boldsymbol{v}\) – скорость среды, \(p\) – давление на границе, \(p_{0}\) – атмосферное давление, \(\boldsymbol{n}\) – нормаль к границе; на нижней – непротекание \(\boldsymbol{v}\cdot\boldsymbol{n} = 0\). Начальные условия соответствовали мгновенному появлению движущегося и вращающегося колеса в покоящихся (в земной системе координат) воде и воздухе. Расчёты производились до установления квазипериодического движения воды и воздуха (более одного оборота колеса).
Применялась подробная квазирегулярная многоблочная расчётная сетка, причём межлопаточные блоки скользили относительно периферийного блока, имеющего форму прямоугольника с вырезанным кругом.
Вычисления проводились с помощью программ ANSYS CFX, для уравнений переноса использовалась численная схема высокого разрешения, для шага по времени обратный метод Эйлера второго порядка, для турбулентности метод первого порядка. В качестве условия сходимости выбрана относительная среднеквадратичная погрешность меньше \(10^{- 4}\).
При вычислении КПД \(\eta\), проводилось усреднение по времени периода входа лопаток (т.е. оборота колеса, делённого на число лопаток), чтобы сгладить выбросы, связанные с временным сдвигом между продольными импульсами и пиками момента торможения колеса.
\[ \eta = \frac {\boldsymbol{F} \cdot \boldsymbol{v}_{v}} {\left|{\boldsymbol{M} \cdot \boldsymbol{\omega}}\right|}, \]
где \(\boldsymbol{M}\) – вращательный момент на валу, \(\boldsymbol{\omega}\) – угловая скорость вращения колеса.
Сила \(\boldsymbol{F}\) вычислялась как интеграл горизонтальных проекций сил давления и поверхностного трения по всей площади контакта колеса с водой.
В качестве параметров воды и воздуха (при \(25\;\text{⁰C}\)) взяты данные из библиотеки материалов ANSYS.
Проводились вычислительные эксперименты по математическому моделированию различных вариантов геометрии неподвижных лопаток при скорости судна \(v_v\) от \(10\) до \(45\;\text{км/ч}\) и скорости вращения колеса, соответствующей максимальной окружной скорости \(v_\omega\) от \(10\) до \(60 \;\text{км/ч}\). На приведённых ниже примерах диаметр колеса \(4\;\text{м}\), скорость судна \(v_v = 45\;\text{км/ч}\), \(v_\omega = 60\;\text{км/ч}\).
Вначале был рассмотрен близкий к традиционному (паром ПКР-25, проекты ледоколов и др. [20; 59]) вариант колеса с ободом и радиально расположенными лопатками (вариант I).
Результаты вычислений (рис. 9, 10) показали, что при указанной высокой скорости судна, во-первых, при входе лопатки в воду создаётся большое усилие, сильный всплеск, который гонит воду как назад, так и вперёд. Во-вторых, между лопатками при их нахождении под водой создаётся разрежение, которое формирует течение к колесу, в т.ч., сзади вперёд в земной системе координат. В-третьих, это разрежение замедляет слив воды при выходе лопаток, и вода ускоряется вверх относительно колеса, т.е. вперёд в земной системе координат. Т.о., при движении постоянно происходит захват части воды с ускорением вперёд до скорости порядка \(v_v\). Другая часть воды получает при гребке скорость порядка скорости скольжения \(\Delta v = v_ω − v_v\), но при необходимых высоких скоростях \(\Delta v \ll v_v\). В результате, суммарный импульс, передающийся воде, в среднем направлен вперёд, а не назад, т.е. сила от колеса (упор) направлена назад относительно скорости судна. В результате, при высокой скорости (например, \(v_v = 45 \;\text{км/ч}\)), эффективность движителя не просто мала, а отрицательна: колесо не ускоряет, а тормозит судно (рис. 10).
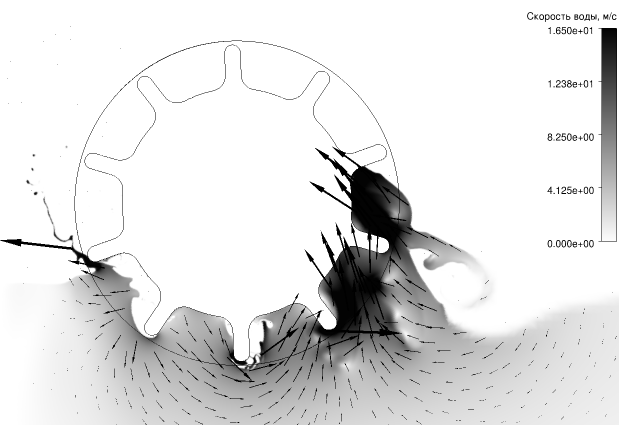
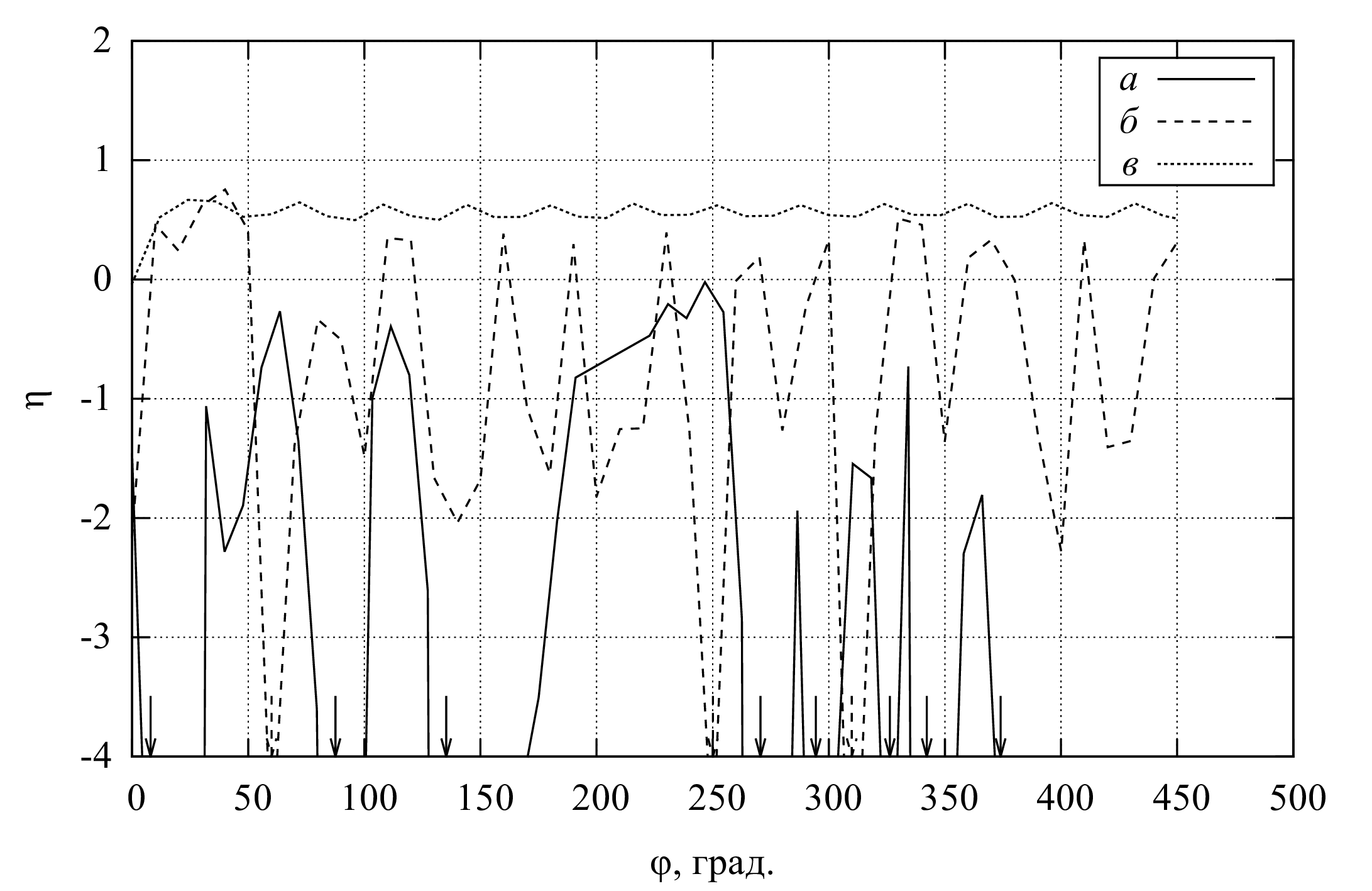
При снижении скорости \(v_v\) до \(10\ldots 15 \;\text{км/ч}\), отрицательные эффекты уменьшаются, и расчётная эффективность \(\eta\) положительна. Отметим, что колёса с такой геометрией лопаток действительно применяются на тихоходных судах.
Другой вариант геометрии (рис. 11) характеризуется лопатками, отделёнными от обода, чтобы давление в межлопаточном пространстве выравнивалось за счёт поступления воздуха со стороны оси вращения (вариант II). По результатам вычислений видно, что эффекты, связанные с разрежением между лопатками, резко ослабляются. Однако при входе лопатки в воду также создаётся большое усилие, локально повышается давление, и формируется течение как назад, так и вперёд. Кроме того, часть воды недостаточно быстро стекает с лопаток и также ускоряется вперёд относительно земной системы координат. В результате при высоких скоростях судна (например, \(v_v = 45 \;\text{км/ч}\)) эффективность движителя оказывается либо недопустимо мала, либо вовсе отрицательна (рис. 10).

В результате анализа вышеуказанного и проведения вариантных вычислений предложена новая геометрия лопаток (вариант III).
Она характеризуется, во-первых, тем, что вместо одиночных лопаток применяются двойные, тройные и пр. лопатки со щелями между ними, через которые вода после гребка сливается с таких лопаток быстрее, чем с одиночных лопаток. Это обеспечивает снижение массы ускоряемой вперёд воды и соответствующей отрицательной составляющей силы, действующей на колесо.
Во-вторых, тем, что внешняя лопатка имеет такой угол наклона относительно соответствующего радиуса, что при заданных \(v_v\) и \(v_\omega\) её внешний край входил бы в неподвижную воду под нулевым углом атаки. Это условие на угол атаки, характерное для оптимальных режимов практически всех лопаточных машин, обеспечивает снижение потерь импульса при входе лопатки в воду.
В-третьих, внутренние лопатки так расположены относительно внешних, что вода, текущая при гребке вдоль внешней лопатки со стороны повышенного давления, проходит по инерции мимо межлопаточной щели и попадает на поверхность внутренней лопатки. Это обеспечивает снижение потерь импульса при гребке из-за протекания воды по щелям.
В-четвёртых, углы наклона внутренних лопаток таковы, что стекающие с внешних лопаток потоки воды, имеющие значительную вертикальную составляющую, направляются внутренними лопатками горизонтально назад. Это снижает потери импульса на вертикальную составляющую.
Результаты вычислений для лопаток с новой геометрией представлены на рис. 10, 12, 13.

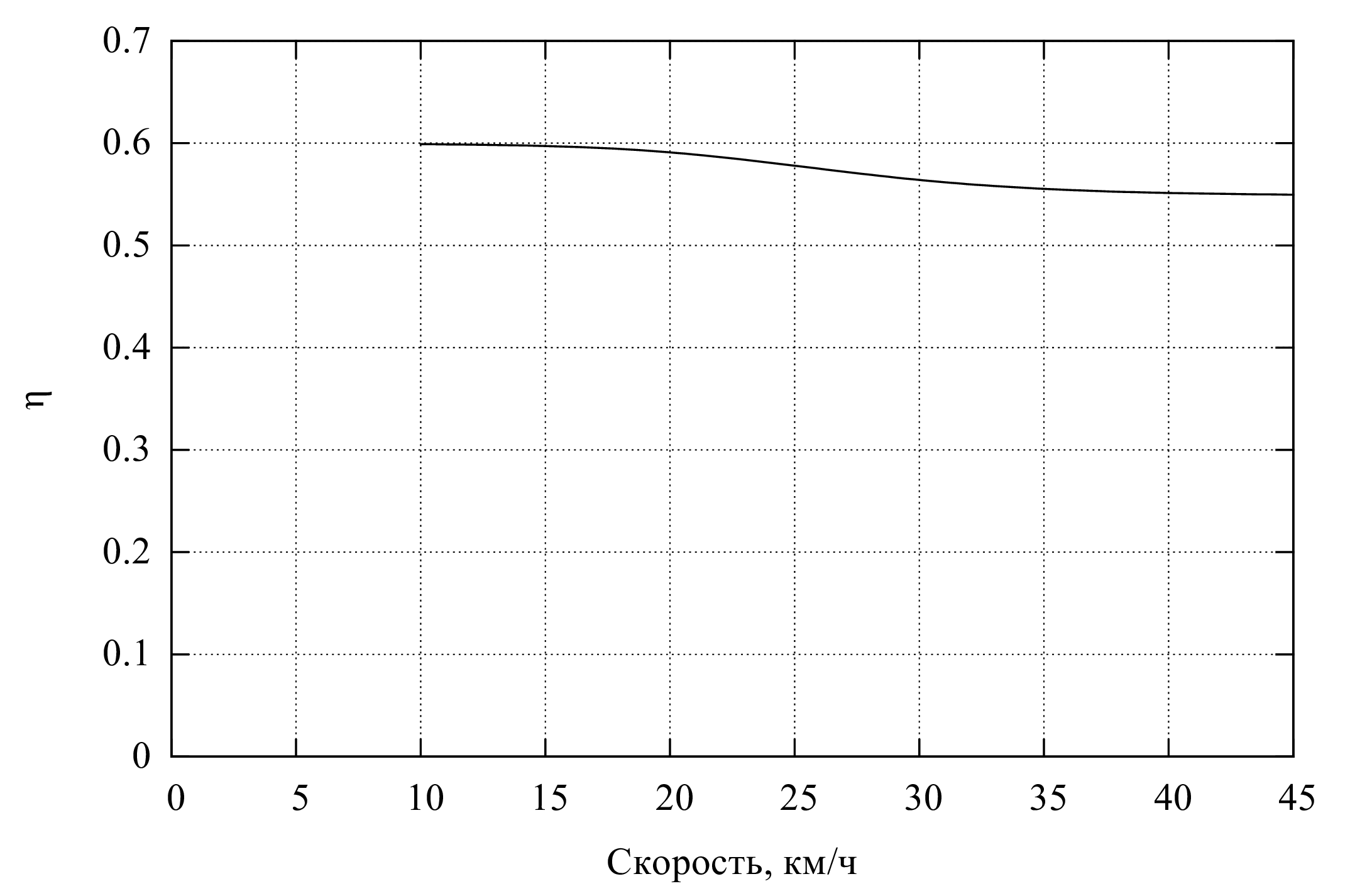
Видно, что, несмотря на то, что воду в месте входа лопатки нельзя назвать неподвижной, погружение происходит без значительного всплеска и без локального повышения давления. Это минимизирует потери на вход.
Вода действительно меньше захватывается и быстрее сливается с нескольких коротких лопаток, чем с одной длинной, что снижает массу захватываемой воды и соответствующие потери импульса.
В то же время, при гребке протекание воды по щелям указанной геометрии затруднено из-за инерционности потоков воды, которые для этого должны поворачивать со значительными ускорениями. Поэтому, как и при сплошных лопатках, создаётся тянущее воду пониженное давление за разрезной лопаткой, а также толкающее воду повышенное давление перед лопаткой. В результате разрезные лопатки обеспечивают эффективность ускорения воды назад. Т.о., щели указанной геометрии не снижают создаваемый упор.
Вертикальная составляющая скорости движения воды, возникающая при гребке после взаимодействия с нижними лопатками, при взаимодействии с верхними лопатками эффективно преобразуется в горизонтальную, что увеличивает горизонтальную составляющую импульса, направленную назад относительно скорости судна, и повышает эффективность движителя.
Видно, что в результате принятых мер гребное колесо оказывается высокоэффективным движителем при высоких скоростях движения судна: значение \(\eta\) при скорости судна \(v_v = 45 \;\text{км/ч}\) достигает \(55\%\). Кроме того, при меньших \(v_v\) оно оказывается даже несколько более эффективно– при условии сохранения вышеописанного соотношения между \(v_v\) и \(v_\omega\), обеспечивающего плавный вход в воду (рис. 13).
Определение геометрии кожуха
В варианте А рассматривается колесо с разрезными скошенными лопатками (рис. 14), показавшее при вычислительных экспериментах высокие характеристики по упору и эффективности при скорости судна до \(45 \;\text{км/ч}\).
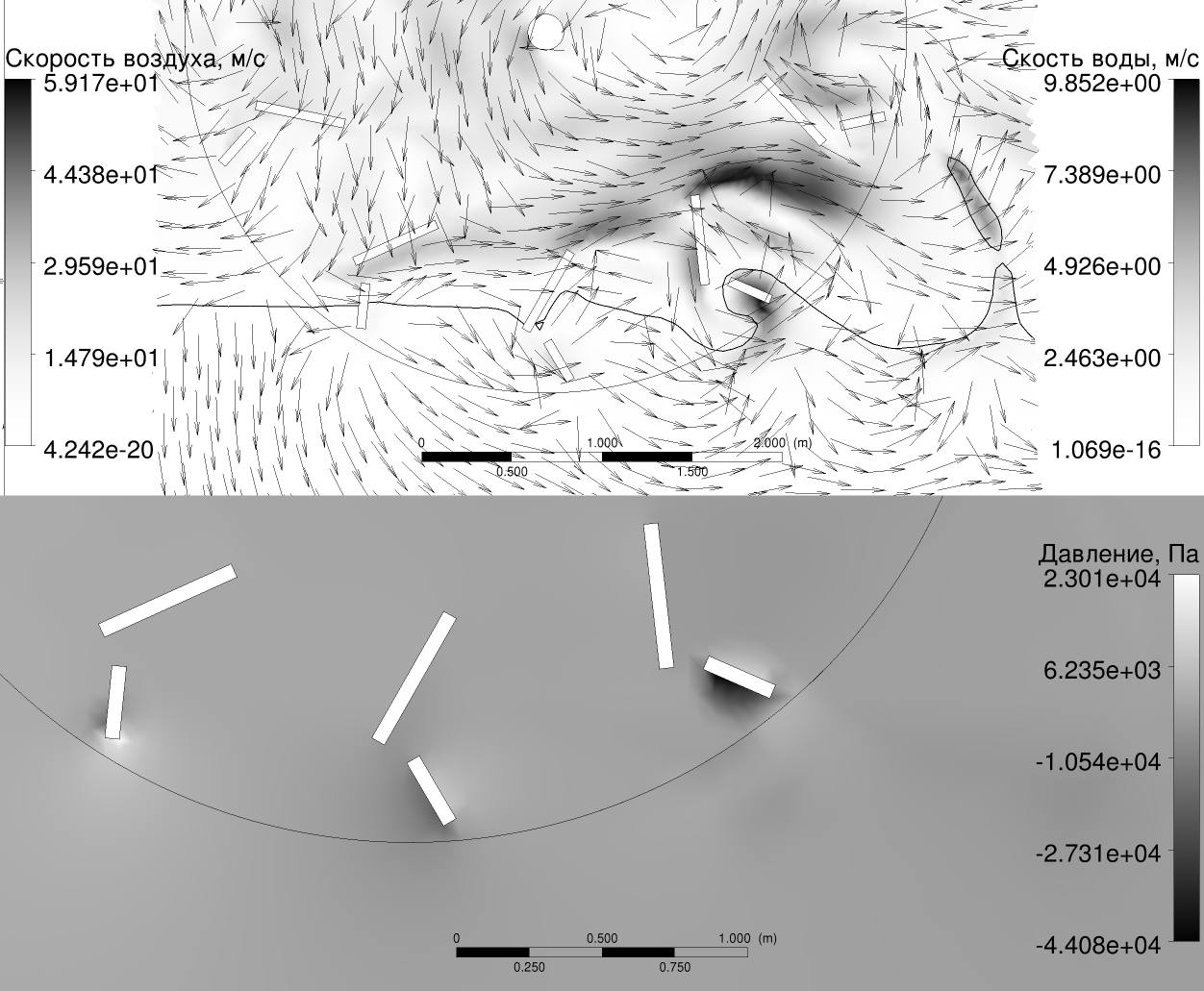
Результаты вычислений (рис. 14, 15) показывают, что взаимодействие с воздухом оказывает значительное тормозящее воздействие как на движение судна, так и на вращение колеса – из-за плохой обтекаемости лопаток.
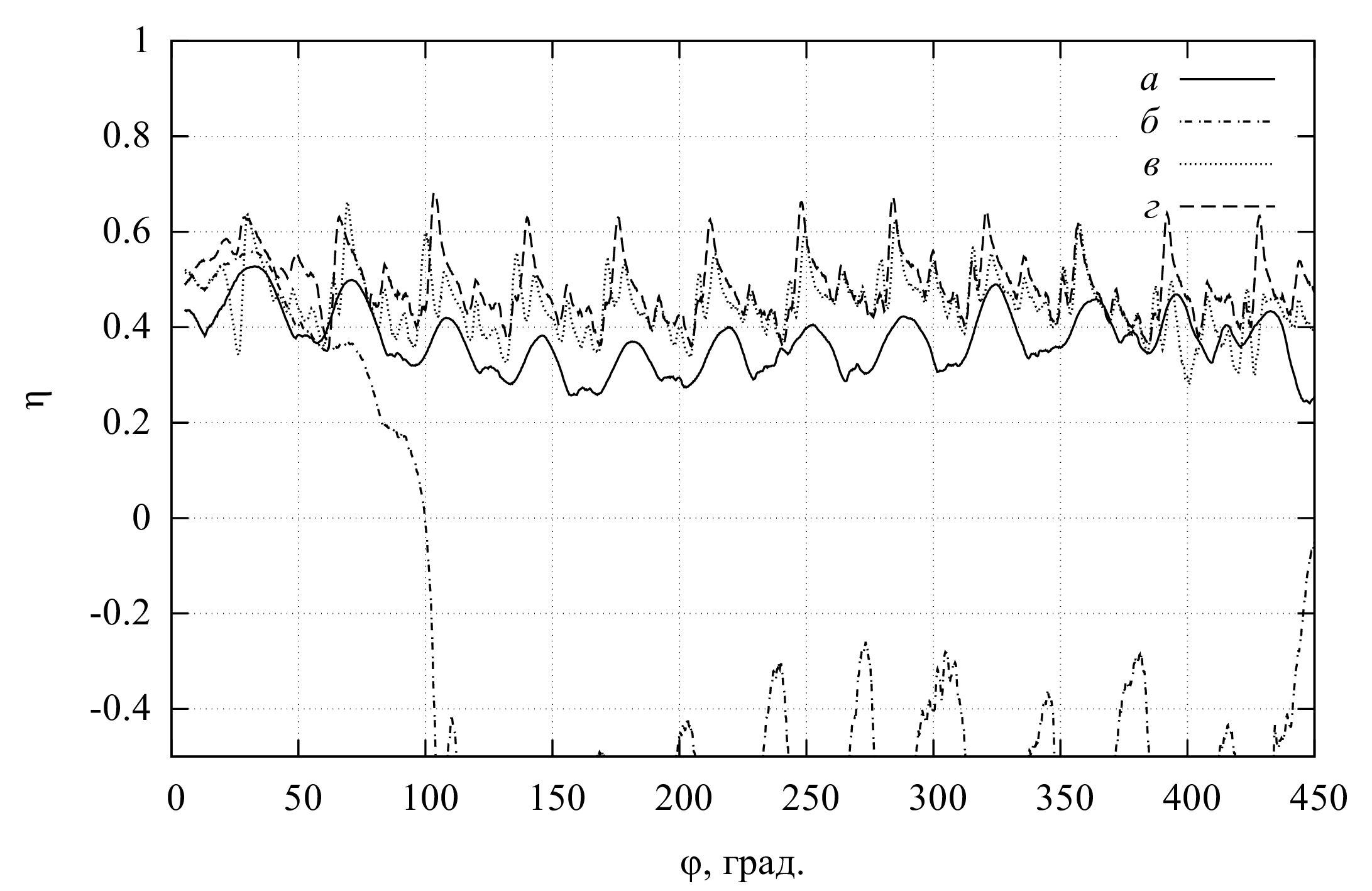
Очевидное решение – закрыть колесо обтекаемым обтекателем (вариант Б, рис. 15, 16).
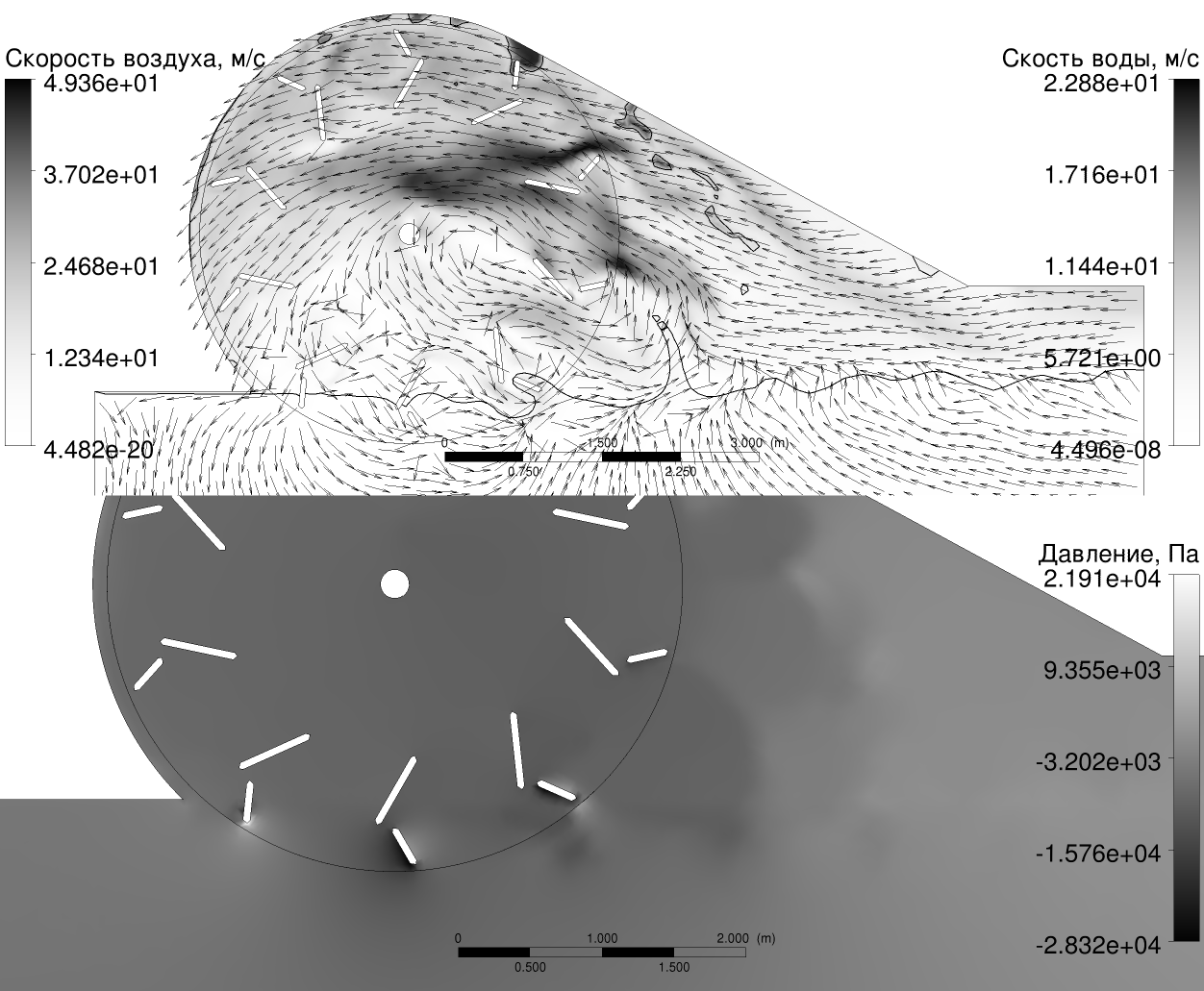
Видно, что внутри обтекателя формируется вихрь, результатом чего становится снижение относительной скорости лопаток и воздуха и соответствующее снижение торможения вращательного движения колеса. Очевидно, снижается и торможение внешнего потока. Всё это оказывает положительное влияние на эффективность колёсного движителя.
Однако возникает новый существенный эффект, связанный с нелинейным взаимодействием воздушной и водной сред. При каждом выходе лопатки из воды формируются более-менее компактные массы воды, поднятые над средним уровнем и ускоренные назад; если при малых скоростях они успевают упасть под действием силы тяжести в пределах объёма обтекателя, то в данном случае высоких скоростей они летят, практически не замечая гравитации. В результате они перекрывают практически всё выходное сечение и “выгребают” воздух из-под обтекателя, где создаётся значительное разрежение. Формирующийся градиент давления захватывает указанные массы воды и ускоряет их вперёд, в направлении движения судна. Это значительно снижает упор и эффективность колёсного движителя.
Для преодоления указанной трудности в варианте В предусмотрено расширение выходного сечения и установка горизонтальных отбойников, разрывающих водяные слои и создающих каналы для прохода воздуха. Отбойники имеют небольшой загиб вниз, чтобы предотвратить частичное расплескивание воды вперёд, наблюдавшееся при взаимодействии с плоскими отбойниками.
Но результаты вычислений (рис. 15, 17) показали, что принятые меры лишь частично уменьшает отрицательный эффект от взаимодействия воздушной и водной сред при встречном течении в выходном канале.
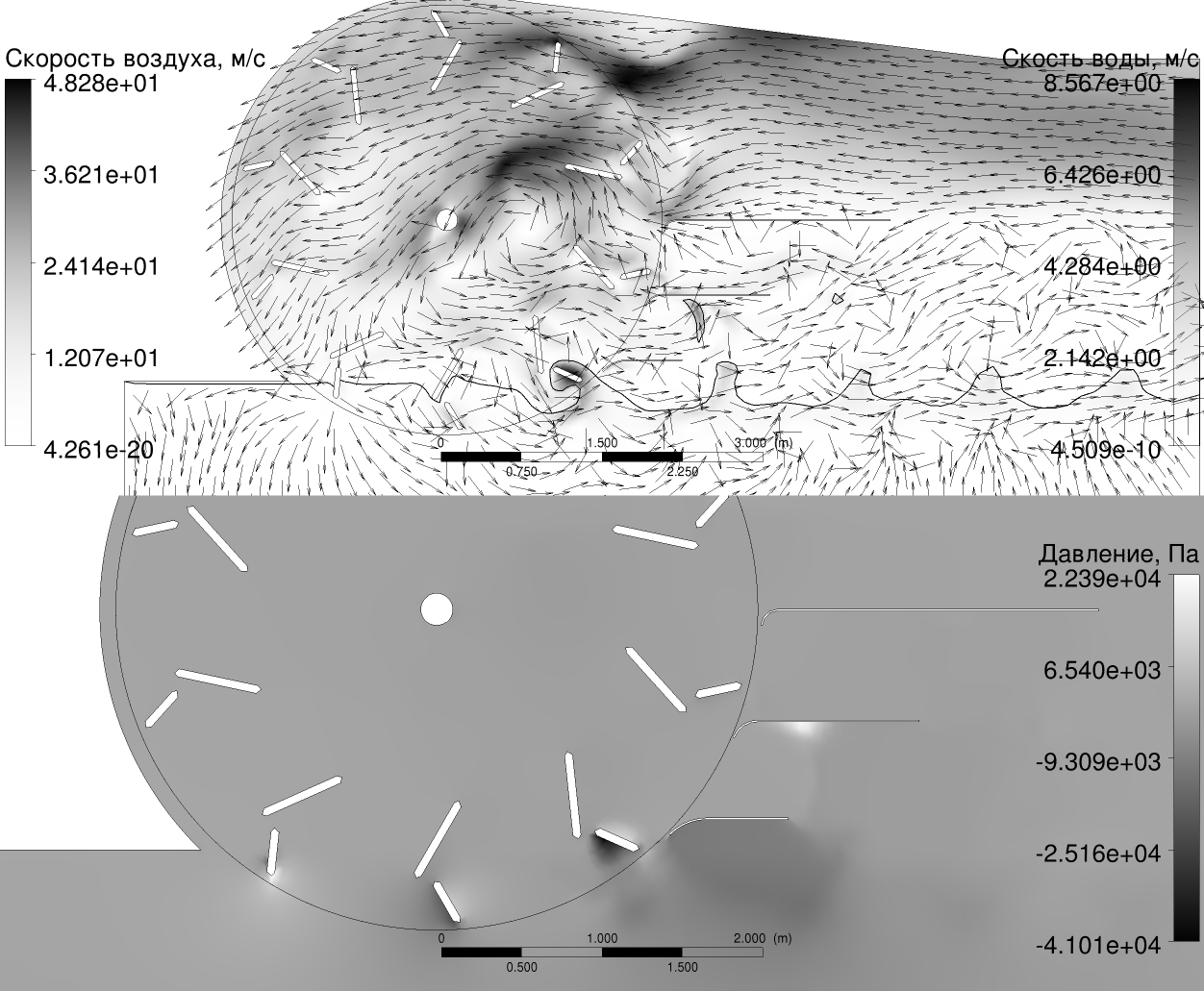
Значительное улучшение ситуации наблюдается при вычислительных экспериментах с вариантом Г (рис. 15, 18). В соответствующей конструкции предусмотрено наличие открытого входа воздуха в нижней колеса, т.е. ограничение обтекателя снизу. Через указанный вход воздух поступает в нижнюю часть колеса, полностью убирая вышеописанный градиент давления.
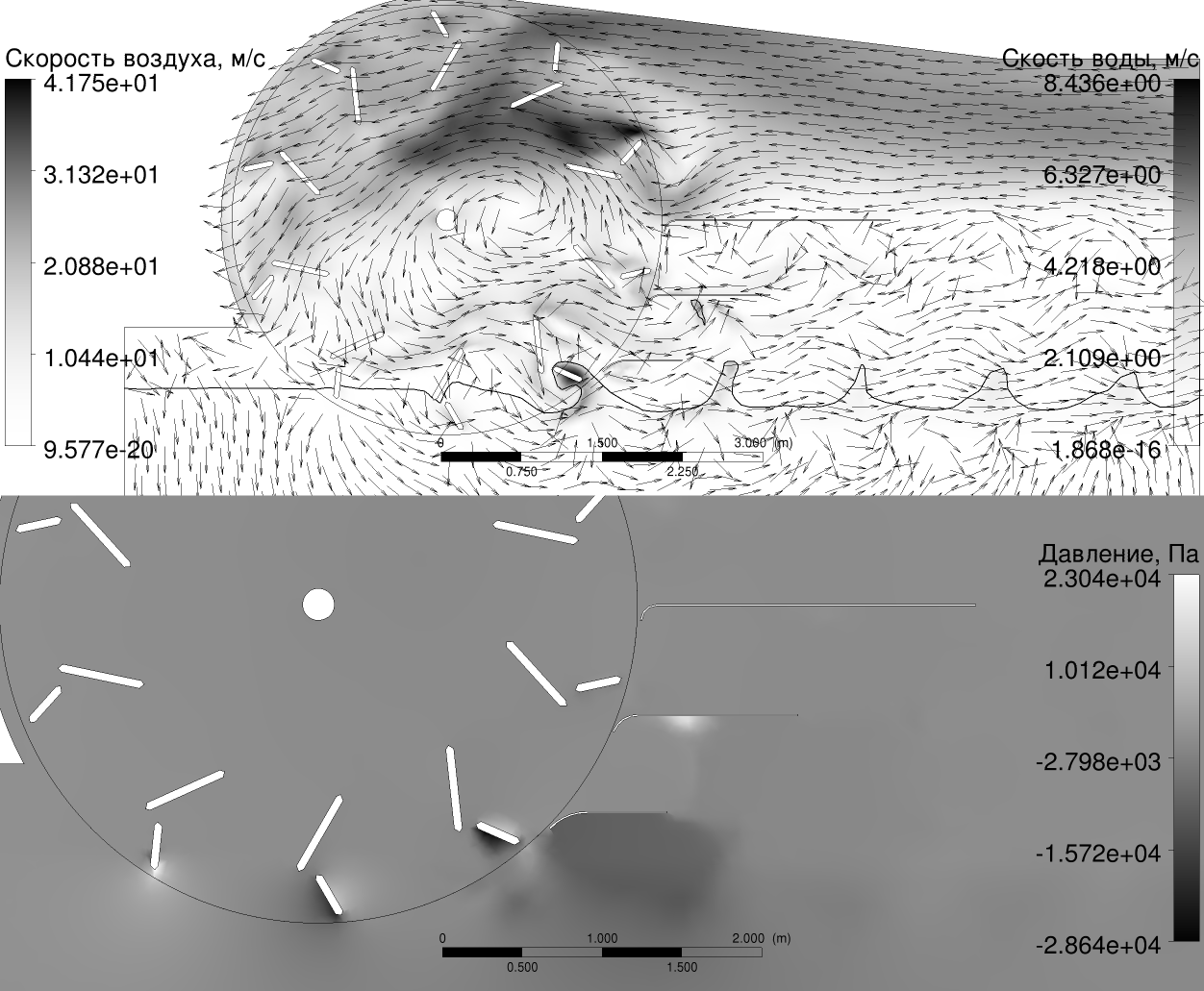
Двигатель и динамика
Расчеты двигателя проводятся исходя из энергетических соображений и литературных сведений о КПД [60]. Мощность двигателя пропорциональна КПД, расходу углеводородного горючего и его теплотворной способности по [61]. Характерные значения КПД задаются графически. Вращение ротора рассчитывается исходя из уравнений динамики для вращения твердого тела вокруг неподвижной оси [62]:
\[P = \varepsilon m' \eta(\omega)\] \[M = \frac{P}{\omega}\] \[\frac{d \omega}{d t} = \frac{M}{J}\]
Здесь \(P\) – мгновенная мощность двигателя, \(\varepsilon\) – теплотворная способность горючего, \(m'\) – массовый расход горючего, \(\eta(\omega)\) – мгновенный КПД двигателя, \(\omega\) – угловая скорость вращения ротора, \(M\) – крутящий момент двигателя, \(J\) – приведенный момент инерции системы относительно оси вращения.
Динамика твердого тела определяется системой уравнений [63].
\[\boldsymbol{v} = \boldsymbol{P}/M\] \[\boldsymbol{\omega} = \hat{I}^{-1}_{lrf}\boldsymbol{L}\] \[ \frac{\mathrm{d}\boldsymbol{x}}{\mathrm{d}t} = \boldsymbol{v}\] \[\frac{\mathrm{d}\boldsymbol{q}}{\mathrm{d}t} = \frac{1}{2}\boldsymbol{\omega} \boldsymbol{q}\] \[\frac{\mathrm{d}\boldsymbol{P}}{\mathrm{d}t} = \boldsymbol{F}\] \[\frac{\mathrm{d}\boldsymbol{L}}{\mathrm{d}t} = \boldsymbol{T}\]
Здесь \(\boldsymbol{P}\) – импульс тела, \(\boldsymbol{L}\) – момент импульса тела, \(\boldsymbol{F}\) – сила, действующая на тело, \(\boldsymbol{T}\) – момент силы, действующий на тело, \(\boldsymbol{q}\) – кватернион вращения тела, \(\boldsymbol{\omega}\) – угловая скорость вращения тела (в виде вектора), \(\boldsymbol{v}\) – скорость движения тела, \(M\) – масса тела, \(\boldsymbol{x}\) – вектор положения центра масс тела, \(\hat{I}^{-1}_{lrf}\) – матрица, обратная матрице момента инерции в СК, связанной с землей, вычисляется по формуле \[\hat{I}^{-1}_{lrf}=\hat{R}\hat{I}^{-1}\hat{R}^{T},\] где \(\hat{R}\) – матрица вращения, по известным формулам построенная из кватерниона \(\boldsymbol{q}\)
\[ \hat{R} = \begin{pmatrix} q_0^2+q_1^2-q_2^2-q_3^2&2q_1q_2-2q_0q_3&2q_1q_3+2q_0q_2\\ 2q_1q_2+2q_0q_3&q_0^2-q_1^2+q_2^2-q_3^2&2q_2q_3-2q_0q_1\\ 2q_1q_3-2q_0q_2&2q_2q_3+2q_0q_1&q_0^2-q_1^2-q_2^2+q_3^2\\ \end{pmatrix}, \]
\(\hat{I}\) – матрица момента инерции тела в системе координат главных осей инерции тела.
Произведение вектора и кватерниона вычисляется по формулам
\[\boldsymbol{\omega}\boldsymbol{q} = \begin{pmatrix} - \sum_{i=1}^{3} \omega_i q_i\\ \omega_1 q_0 - \omega_2 q_3 + \omega_3 q_2\\ \omega_1 q_3 + \omega_2 q_0 - \omega_3 q_1\\ - \omega_1 q_2 + \omega_2 q_1 + \omega_3 q_0 \end{pmatrix} \]
Методика расчета комплекса
При помощи вспомогательного программного обеспечения [64], полученные системы уравнений для каждой из отдельных моделей из раздела переписываются в общих терминах и упорядочиваются для вычислений. Шаг по времени для дифференциальных уравнений рассчитывается с Ньютоновским решателем для плотных матриц и шагом по времени по формуле обратного дифференцирования [26].
Математическая модель АСВП классического типа с таким количеством взаимосвязанных рабочих и сопутствующих процессов разработана, по-видимому, впервые. Для описанных инновационных АСВП вычисления ранее не проводились.
Надёжность общей комплексной модели АСВП обоснована тем, что алгоритм вспомогательного программного обеспечения обеспечивает полную адекватность алгоритмов программных блоков комплексной модели соответствующим отдельным моделям, в отдельных моделях применены отработанные соотношения, прошедшие согласование с экспериментами, а также проведено сопоставление характеристик реального АСВП классического типа [3] с соответствующей комплексной моделью.
В интересах разработки СВП были проведены прогнозные вычисления по комплексным математическим моделям для СВП разных масштабов с классическими и инновационными ГО и движителями, различными компоновками и значениями проектируемых параметров, с разными траекториями и ускорениями над твердыми и жидкими поверхностями с разными неровностями, с препятствиями разных форм и размеров.
Часть 3. Результаты моделирования
Экспериментальные и конструкторские разработки СВП новых типов
С помощью вышеописанных математических моделей проведен ряд экспериментальных и конструкторских разработок по программе создания СВП (рис. 19-21). Разработанные технические решения реализованы в полномасштабном опытном образце ТСВП массой около \(4,9\;\text{т}\) с гибридным опорным ходовым комплексом.



Для примера приведем некоторые технические характеристики транспортного СВП средней грузоподъемности, разрабатываемого нами в рамках ОКР «Север» (рис. 21): полная масса \(32,0\;\text{т}\), грузоподъемность \(10,0\;\text{т}\), длина \(25,9\;\text{м}\), ширина \(13,6\;\text{м}\), погрузочная высота \(1,2\;\text{м}\), площадь грузовой платформы \(127,0\;\text{м}^2\), высота преодолеваемого уступа (волны) \(2,0\;\text{м}\), преодолеваемый подъем \(21,0^\text{o}\), максимальная скорость \(45\;\text{км/ч}\).
Максимальное давление ТСВП на грунт со стороны ВП в режиме частичной разгрузки \(206\;\text{даН/м}^2\) (при поднятых колесах \(340\;\text{даН/м}^2\))
Т.о., сделан значительный задел по созданию инновационных конструкций СВП, удовлетворяющих требованиям эксплуатации в условиях Крайнего Севера.
Результаты вычислительных экспериментов
Расчеты по вышеописанной комплексной математической модели АСВП применялись для исследования различных типов АСВП; ниже приведены результаты вычислений для примеров:
Легкого АСВП классического типа (АСВП КТ) массой 18 тонн (освоенный диапазон параметров АСВП – для верификации математической модели)
Тяжелого АСВП КТ массой 200 тонн (для математического обеспечения при разработки нового АСВП в рамках НИР «Амфибия»)
Инновационного АСВП с контактными колёсными движителями, гребными колёсами и ГО из отдельных конусов.
Рассматривались варианты с различными сценариями движения (разгон, маневрирование, прямолинейное движение по пересеченной местности), видом подстилающей поверхности (глубокая вода, твердая поверхность), ее формой (ровная горизонтальная и наклонная, волнистая, мелкие и относительно крупные хаотические неоднородности, рис. 22), рассматривалось преодоление крупных препятствий различной формы (что важно для применения АСВП в условиях Арктики, где приходится учитывать наличие торосов).
Волны на глубокой воде моделируются в соответствии с [65]. В приводимых далее примерах рассматривались волны для случая скорости ветра 2.7 м/с на высоте 10 м над уровнем моря. Неровности твердой поверхности задавались с помощью генератора случайных чисел с максимальным перепадом между вершинами и впадинами 20 см и характерным размером по горизонтали 1 м и 5м (малоразмерные и крупные неровности).
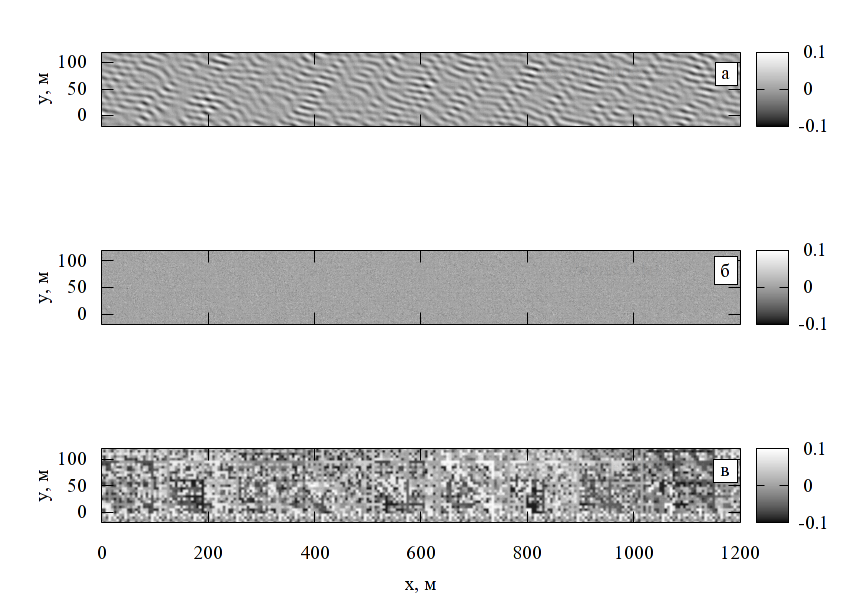
Легкое АСВП КТ
Приведенные ниже результаты расчетов соответствуют следующему варианту конструкции.
Гибкое ограждение имеет прямоугольную форму и состоит из 60 элементов. Ширина ГО 8.2 м, длина 19 м, высота 1.7 м. Угол наклона навесных элементов θ=45⁰. Ширина навесных элементов – 30 см. В воздушном тракте за нагнетателями характерная поперечная площадь сечения принималась равной 1 м2, а характерная длина пути – 10 м.
АСВП КТ снабжено двумя винтовыми воздушными четырехлопастными движителями с радиусом 3 м. Длина хорды лопасти винта 0.2 м, радиус кока 0.35 м, угол крутки φ(r) = (0.15 R/r + π/10) рад. Каждый винт имеет по три лопатки рулей с длиной хорды 0.3 м. В данном примере выбран профиль лопаток СибНИА С-11.
Рассматривались варианты с аэродинамическим коэффициентом лобового сопротивления cx = 0.7 и 0.35.
Режим работы двигателя для нагнетателей подбирался исходя из стабильной штатной работы воздушной подушки. Для всех вариантов подстилающей поверхности, парение стабильно при расходе горючего на работу компрессоров около 72 кг/ч. Средняя ширина зазора составляет 13 см при парении над водой и 10 см при парении над твердой поверхностью.
При разгоне задавалось нарастание расхода горючего на работу движителей. Первые 10 секунд до 90% максимального значения, и далее плавный выход на максимум 54 кг/с в течение 20 секунд. При этом движители выходят на квазистацонарный режим с задержкой 7..10 с. Сила тяги проходит через максимум из-за особенностей взаимодействия винта с набегающим потоком. В начале разгона (3..5 с) наблюдаются колебания АСВП в вертикальном направлении и соответствующие колебательные изменения зазоров гибкого ограждения, связанные с отличием значений стартовых параметров от равновесных. С ростом скорости импульсное и профильное сопротивления возрастают, а остаточное, волновое и струй – проходят через максимум, но суммарное сопротивление возрастает монотонно (рис. 24). За 60 секунд судно разгоняется до скорости 34.5 км/ч (рис. 23, а). Квазистационарная скорость при данном расходе топлива составляет 45 км/ч.
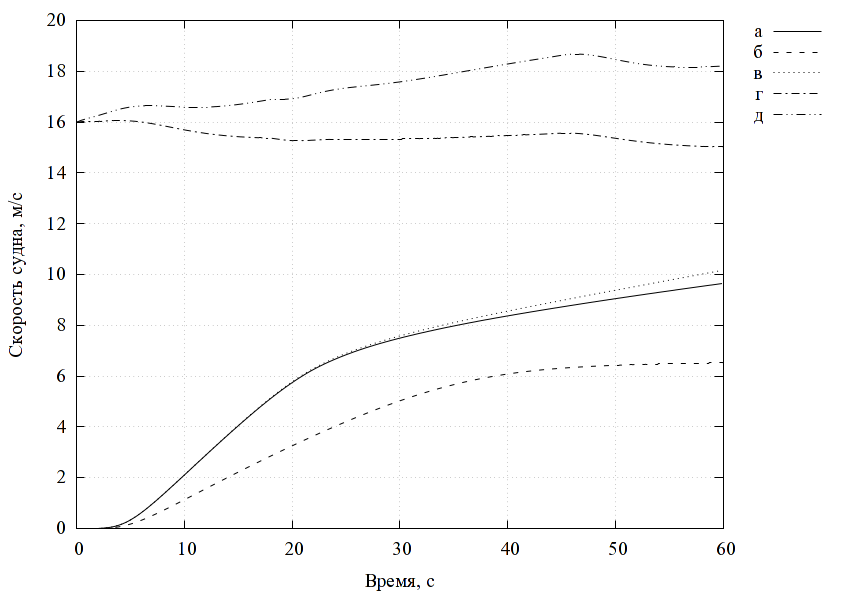
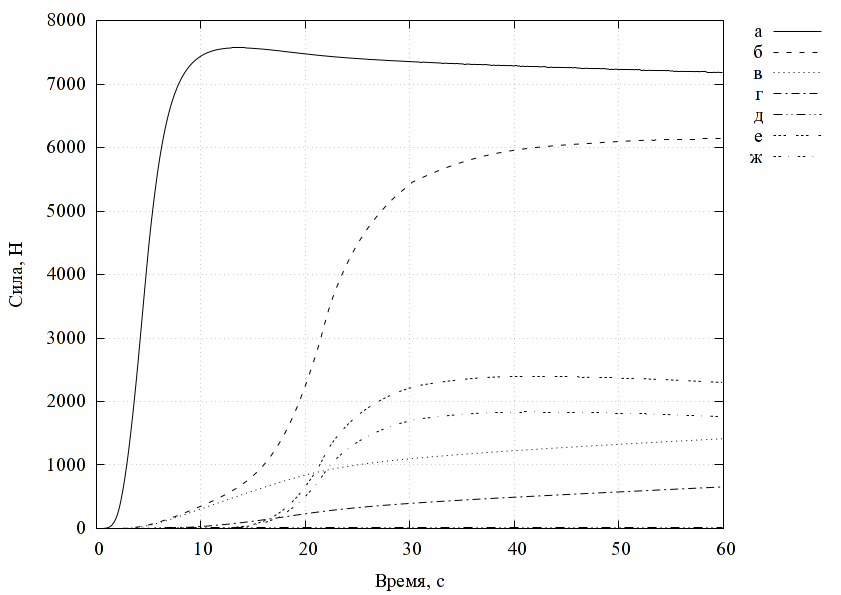
При понижении максимального расхода топлива до 27 кг/ч, АСВП не преодолевает максимум волнового и остаточного сопротивления, что приводит к стаблилизации скорости на уровне 24 км/ч (рис. 23, б)
При пониженном коэффициенте аэродинамического сопротивления, предсказуемо снижаются составляющие профильного сопротивления (рис. 25). Однако, поскольку последнее составляет относительно небольшую часть общего сопротивления, это практически не сказывается на скоростных характеристиках АСВП (рис. 23, в).
При маневрировании на различных подстилающих поверхностях, расход горючего двигателем движителя фиксируется на уровне 54 кг/ч. Рули управляются ПИД-регулятором , оперирующим углом рыскания судна с параметрами P=1.2, I=0.1, D=3.6.
Типичные траектории движения приведены на рис. 26
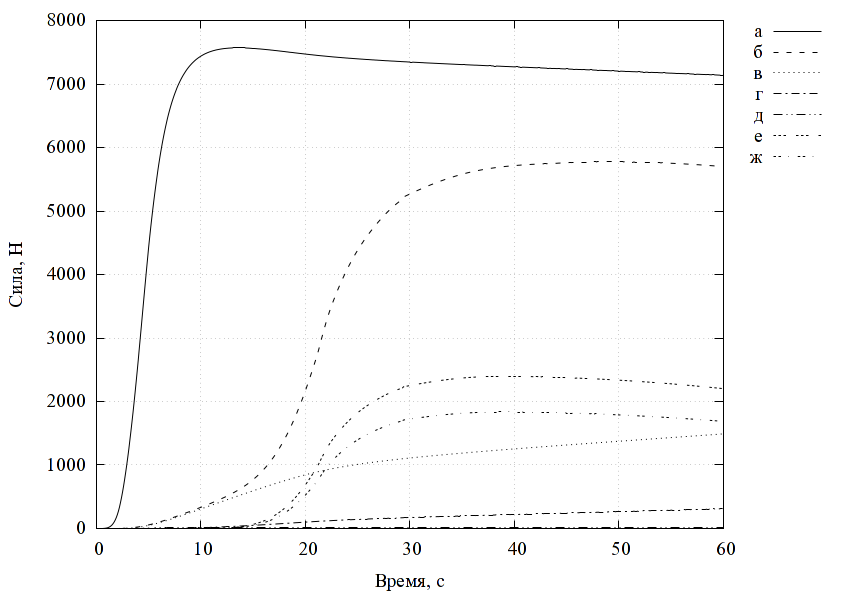
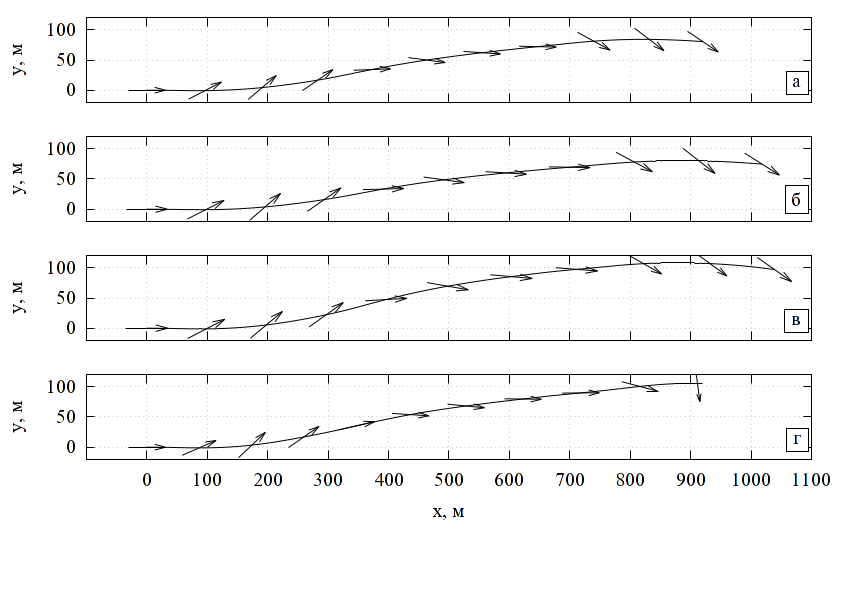
Сила тяги движительно-рулевого комплекса при повороте рулей уменьшается за счет роста сопротивления рулевых поверхностей (рис. 27, а). Отрицательную роль играет так же изменение направления набегающего на винт потока. В результате, при маневрировании во время движения АСВП “боком”, скорость снижается, а при выравниивании относительно курса – снова растет (рис. 23, г, д).
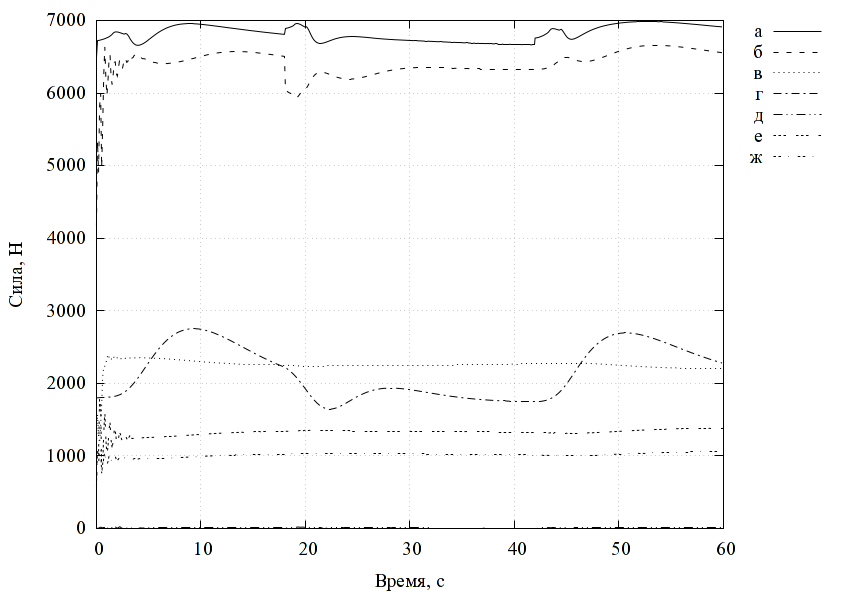
В моменты резкого изменения положения рулей возникают возмущения многих характеристик подсистем АСВП. Наблюдается нестационарный крен АСВП, изменение тангажа, зазоров под элементами ГО, расходов и давления в секциях, резкие иземенения модуля силы профильного сопротивления, возмущения прочих компонент сопротивления и др. (рис. 27)
Маневрирование на твердой ровной поверхности отличается от ровной водной отсутствием волнового и остаточного компонент сопротивления. В результате, при маневрировании судно разгоняется до 66 км/ч (рис. 23, д)
При маневрировании над неровной поверхностью, происходит модуляция расхода через элементы гибкого ограждения в соответствии с локальной мгновенной формой подстилающей поверхности. Как следствие, возникают осцилляции расхода через нагнетатели, давления в секциях, возникают вертикальные колебания центра тяжести корпуса, осциллируют крен и тангаж (рис. 28, а, б). Частота колебаний связана в основном с размером неоднородностей поверхности. В силу инерционности системы, амплитуда колебаний зависимых характеристик понижается с повышением частоты. Автоматическое управление положением рулей подавляет колебания по курсу, как следствие, по углу рыскания частота колебаний значительно ниже (рис. 28, в).
Тяжелое АСВП КТ
В этом примере гибкое ограждение имеет прямоугольную форму и состоит из 200 элементов. Ширина ГО 15 м, длина 35 м, высота навесных элементов 1 м. Угол наклона навесных элементов θ=45⁰. Ширина навесных элементов – 50 см.
АСВП снабжено четырьмя винтовыми воздушными четырехлопастными движителями с радиусом 1.5 м, расположенными по углам корпуса. Длина хорды лопасти винта 0.5 м, радиус кока 0.35 м, угол крутки φ(r) = 0.08 R/r рад. Поворот осуществляется поворотом движителей вокруг вертикальной оси.
Аэродинамический коэффициент лобового сопротивления cx = 0.4, аэродинамический коэффициент поперечного сопротивления cx=0.5.
Для всех вариантов подстилающей поверхности, кроме твердой поверхности с крупными неоднородностями, парение стабильно при расходе горючего на работу компрессоров 324 кг/ч.
Средняя ширина зазора при парении над ровной поверхностью 3,5 см, над ровной водной поверхностью – 7,7 см.
Ниже приведены результаты расчетов разгона на волнующейся воде для различных направлений ветра (встречный и поперечный).
При разгоне по ровной твердой поверхности, судно разгоняется до крейсерской скорости 72 км/ч за 60 секунд (рис. 29, а). Расход топлива на работу движителей на крейсерской скорости – 72 кг/ч.
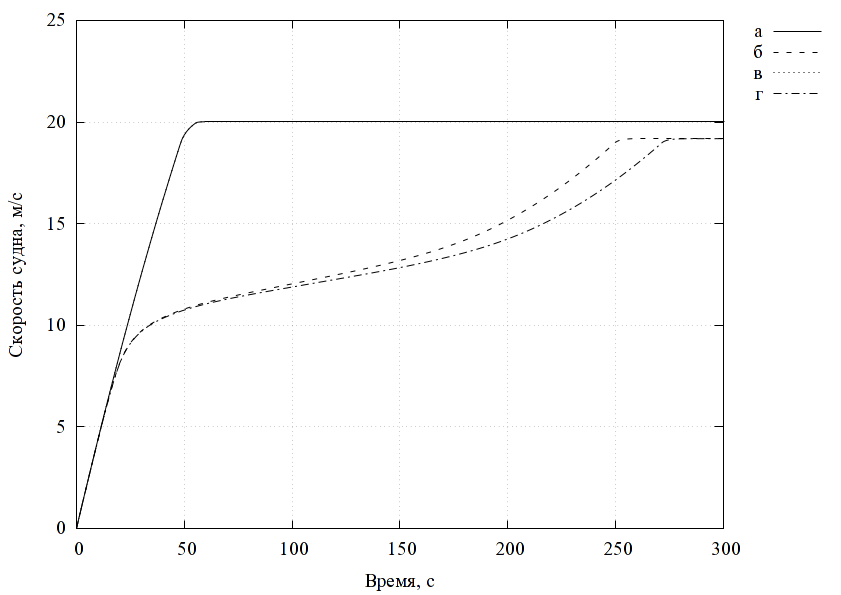
Разгон по твердой поверхности с мелкими неоднородностями в целом аналогичен (рис. 29, в), за исключением наличия выскокочастотных колебаний различных параметров (в т.ч. вертикальных вибраций), связанных с неровностью поверхности. (рис. 28, г, д).
При разгоне по ровной водной поверхности, за 60 секунд судно достигает половины крейсерской скорости и далее постепенно разгоняется до крейсерской в течение 3-4 минут (рис. 29, б). При этом вклад гидродинамических компонент сопротивления в суммарное оказывается решающим (рис. 30). Расход топлива в процессе разгона в среднем составляет 612 кг/ч. Расход топлива на крейсерской скорости – 382 кг/ч.
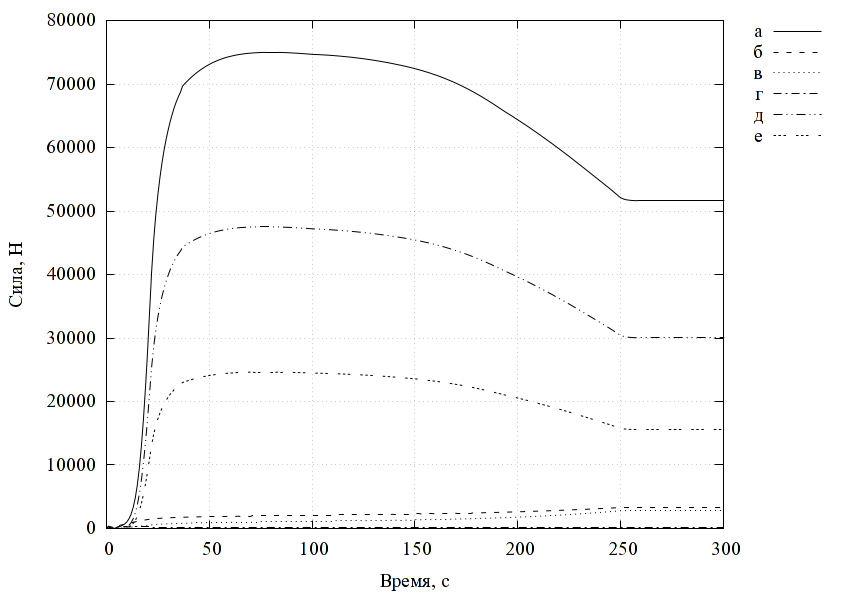
Примечательно, что в данном примере суммарное сопротивление проходит через максимум при скоростях около 40 км/ч, т.е. для повышения топливной эффективности двигаться АСВП по воде следует либо с малыми скоростями – до 36 км/ч, либо быстрее 54 км/ч.
При разгоне на волнующейся воде, возникают колебания характеристик, связанные с неровностью поверхности. Это приводит к значительной тряске (рис. 28, ж, з), однако в остальном влияет на поведение судна слабо (рис. 28, и, 29, г). При поперечном ветре, возникает дрейф, связанный с вкладом профильного сопротивления ветру (поперечная скорость достигает 3,6 км/ч). При встречном ветре, возрастает вклад профильной и импульсной компонент сопротивления, и преодоление пика сопротивления оказывается затруднено. В результате, разгон до крейсерской скорости занимает 16 минут, а расход топлива на крейсерской скорости возрастает до 418 кг/ч.
Рассматриваись сценарии маневрирования над гладкими водной и твердой поверхностями, над поверхностю с крупными неоднородностями и над волнующейся водой при попутном ветре 2,5 м/с. Траектория движения для всех подстилающих поверхностей приблизительно одинакова. Типичный образец приведен на рис. 31.
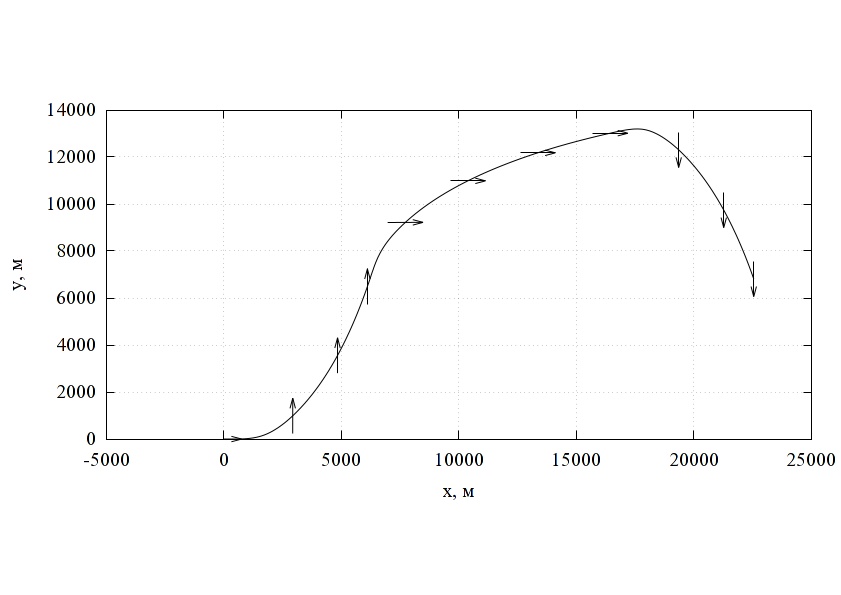
Видно, насколько АСВП инерционно: поворот происходит на расстоянии порядка 5 км, при поворотах скорость судна снижается мало, для выполнения поворота АСВП долгое время должно двигаться под углом к курс�� порядка 45⁰. При маневрировании над твердой поверхностью скорость судна варьируется в диапазоне от 70 до 73 км/ч, а над водой – от 68 до 69 км/ч.
В ряде случаев при более резких поворотах моделировалась аварийная ситуация – переворот АСВП.
Инновационное АСВП для российского Севера
В соответствии с приведённым выше анализом, перспективна разработка АСВП инновационной конструкции, содержащее частично разгруженные колёсные контактные движители для движения по твёрдой поверхности, конические элементы ГО для формирования воздушной подушки, и гребные колёса новой конструкции для движения по воде и болотистой местности.
На рис. 33-36 для такого инновационного АСВП представлены некоторые результаты вычислений по комплексной модели. Масса АСВП 50200 кг, аэродинамические коэффициенты по осям x и y – 0.4 и 0.5. Основные характеристики ходовой части: Ширина и диаметр гребных колес: 4 м, Момент инерции 0.0146 кг·м². Для обычных колес диаметр 4 м. Момент инерции 7200 кг·м². Коэффициент реакции поверхности 107 Н/м. Коэффициент трения поверхности 1. Коэффициент вязкого трения вращения в колесах 1 1/с. Коэффициент амортизации 2500 Н·с/м Коэффициент жесткости пружины амортизатора 250000 Н/м. Масса колеса 2000 кг. Коэффициент передачи с двигателя колеса на само колесо 25. Диаметр нижнего торца большого конического элемента ГО 6.04 м, малого – 4.2 м.
На твердой поверхности при скорости 45… 47 км/ч поворот происходит на расстоянии порядка 20 м, как у автомобиля. Бертеновские конуса создают 120 кН подъёмной силы, колёсные контактные движители – 360 кН, при этом избыточное давление в ГО составляет порядка 1 кПа, т.е. 1% от атмосферного. САУ задвижки существенно сокращает колебания ГО и АСВП в целом, вертикальные колебания амплитудой 5 мм, частотой 1 Гц. Расход горючего двигателей колёсных контактных движителей составляет 230,4 кг/ч.
Хорошая управляемость такого АСВП продемонстрирована также на других траекториях и формах твёрдых поверхностей, в т.ч. гладких с уклонами, с малоразмерными и крупными неоднородностями.
Расчёты показали, что при необходимости (например, при движении по летней тундре) давление легко может быть повышено, по крайней мере, в 3 раза, при этом давление на грунт ниже допустимого с экологической точки зрения, а остаточная сила на разгруженные колёса остаётся достаточной для движения АСВП, правда, с несколько меньшей скоростью.
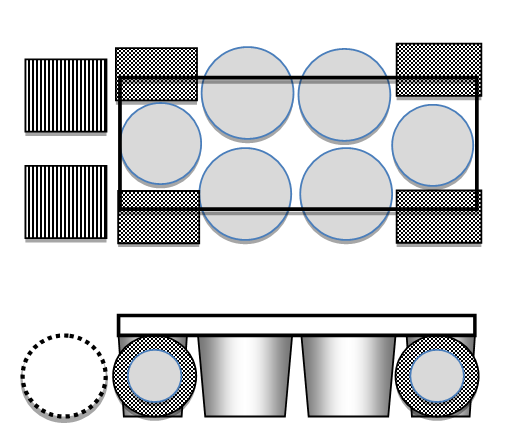
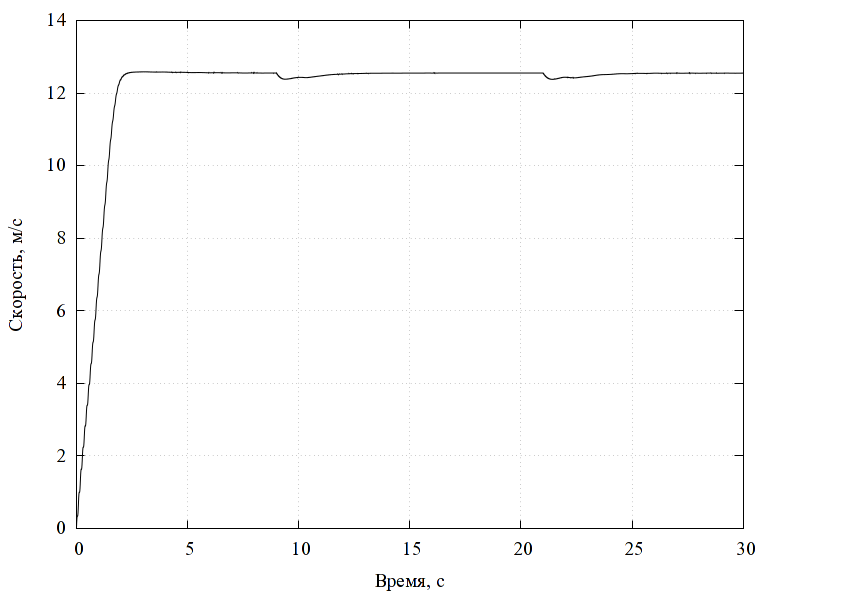
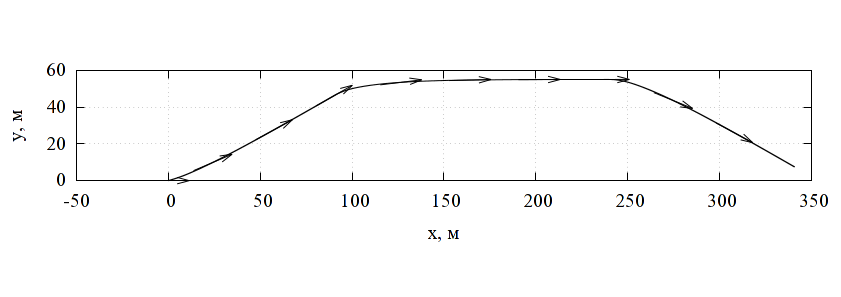
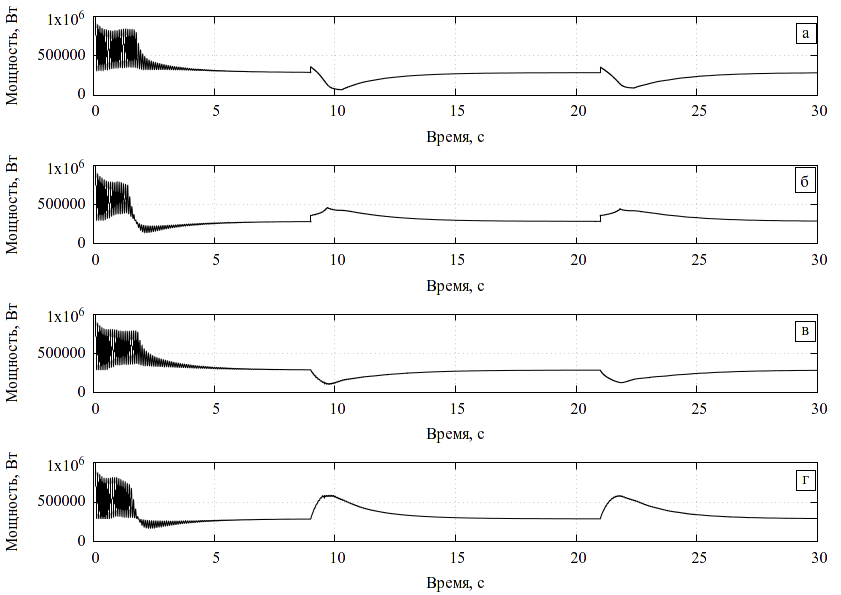
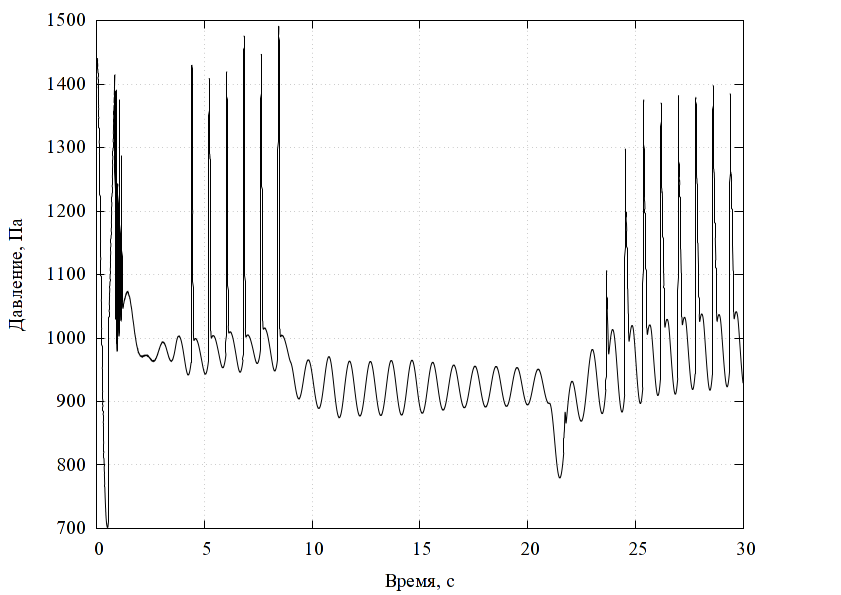
Моделировался наезд АСВП на крупномасштабное препятствие (аналоги торосов, валуна, берегового уступа и др.). Очевидно, локальные зазоры резко увеличиваются, и поддерживающее давление в соответствующих элементах воздушной подушки спадает. Однако во многих случаях АСВП проходит препятствия высотой порядка метра из-за автоматического перераспределения поддерживающих сил от колёсных движителей (сжатие пружинных элементов) и от не контактирующих с препятствием автономных конических элементов гибкого ограждения (уменьшение зазоров и рост давления в элементах воздушной подушки).
Некоторые результаты расчётов движения АСВП по воде показаны на рис. 37 для примера разгона по гладкой воде от средних скоростей к высоким. Видно, что АСВП разгоняется за несколько секунд, средний упор гребных колёс плавно растет с увеличением скорости и связанных с этим сопротивлений, при этом КПД примерно постоянен (около 50%). Несмотря на значительные выбросы во временных зависимостях сил при гребках, центр масс вибрирует незначительно.
Т.о., описанная инновационная конструкция АСВП обеспечивает энергетически эффективное движение как по твёрдой, так и по водной поверхности, и позволяет преодолевать крупные препятствия. По указанным характеристикам, существенным для транспортных средств российского Севера, она намного превосходит АСВП классического типа, при этом сохраняются.
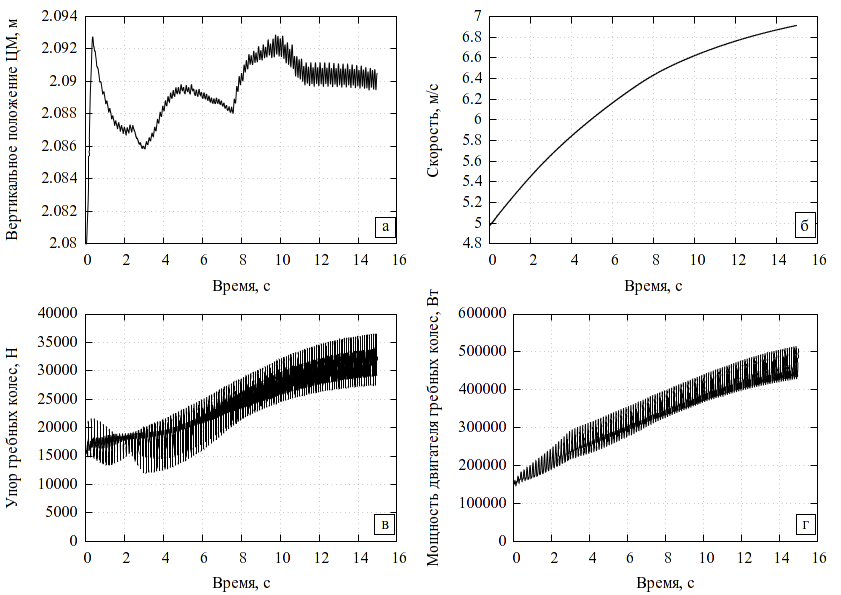
Заключение
Разработано программное обеспечение, которое, по-видимому, лучше других удовлетворяет комплексу требований для математического моделирования технически сложных объектов, состоящих из подсистем, рабочие процессы в которых относятся к различным областям знаний и моделируются различными автономными группами исследователей с различной степенью подробности (в т.ч. с использованием подходов иерархического моделирования и табличного задания процессов). Язык разработки автономных моделей подсистем общеизвестный – C++, переносимый на большинство популярных платформ, что снижает порог вхождения новых групп исследователей.
Предложено гребное колесо новой конструкции обладает качествами, критически важными для применения, в т.ч., в условиях Крайнего Севера. Значительный интерес представляет разработка движителей с применением гребных колес для вновь создаваемых судов амфибийного типа. Средняя эффективность такого движителя, определённая с учётом сопротивления воздуха, при скорости судна \(45 \;\text{км/ч}\) достигает \(48\%\). Это может сделать такие движители конкурентоспособными для широкого класса судов. Конечно, этот вывод, полученный с помощью вычислительного эксперимента, следует проверить на физических и натурных испытаниях, но перспективы представляются многообещающими.
Из анализа природных, экологических и социально-экономических условий применения транспортных средств на крайнем Севере следует перспективность разработки амфибийных судов на воздушной подушке АСВП. Разработан математический аппарат для концептуального проектирования как АСВП классического типа, так и АСВП, содержащих инновационные технические решения: гибкое ограждение, состоящее из отдельных конусов, колёсные контактные движителии новые, высокоэффективные гребные колёса с высоким тяговым КПД как на малых, так и на высоких скоростях (до 45 км/ч). Для условий Севера показана целесообразность разработки инновационного АСВП.
Литература
1. Попов С.Д. Фундаментальные Проблемы Развития Внутреннего Транспорта Малонаселенных Регионов России и Пути Ее Решения На Основе Развития Высокомобильных Автомобильных Транспортных Комплексов (На Примере Архангельской Области) / С.Д. Попов // Сб.Статей По Итогам Международной Научно-Практической Конференции. Экономика, проектный менеджмент, образование, юриспруденция, экология, медицина, социология, философия, филология, психология, техника, математика: состояние и перспективы развития. – СПб: КульИнформПресс, 5BC–2013. – P. 110-117.
2. Чеботаев А.А. Безвредные Транспортные Средства Для Севера / А.А. Чеботаев, А.Д. Мельник // Сб. Матерталов Всесоюзной Научно-Практической Конф. 23–26 Октября 1990 Г Научно-технический прогресс и перспективы развития новых специализированных видов транспорта. – М.: ВНИИПК техоргнефтегазстроя, 1990. – Vol. 2. – P. 115-125.
3. Демешко Г.Ф. Проектирование Судов. Амфибийные Суда На Воздушной Подушке Книга 2 / Г.Ф. Демешко. – СПб: Судостроение, 1992. – 329 p.
4. Попов С.Д. Проектирование и Комплексное Математическое Моделирование Судна На Воздушной Подушке Для Регионов Севера, Сибири и Арктического Континентального Шельфа. / С.Д. Попов, С.Н. Чувашев // Инженерный журнал: наука и инновации. – 2013. – № 3 (15). – P. 9.
5. Belousov B.N. Heavy-duty wheeled vehicles: Design, theory, calculations. Heavy-duty wheeled vehicles / B.N. Belousov. – Warrendale, Pennsylvania, USA: SAE International, 2014. – 553 p.
6. Попов С.Д. Некоторые Проблемы Создания Амфибийных Транспортных Систем, Предназначенных Для Решения Транспортных Задач и Освоения Труднодоступных Регионов Севера и Сибири, а Также На Арктическом Шельфе. / С.Д. Попов // Материали За 9-а Международна Научно-Практична Конференция Achievement of high scool. – София «Бял ГРАД-Ы» ООД, 2013. – Vol. 45. – P. 104.
7. Попов С.Д. Разработка Технологии Выбора Несущего Комплекса Для Транспортных Средств На Воздушной Подушке (ТСВП), Предназначенных Для Эксплуатации На Севере и в Сибири / С.Д. Попов, С.Н. Чувашев // Сб. Статей Международной Научно-Практической Конференции Инновационное развитие современной науки / ed. А.А. Сукиасян. – Уфа: РИЦ БашГУ, 2014. – Vol. 3. – P. 287-295.
8. Попов С.Д. Разработка Технологии Математического Моделирования Некоторых Опасных Ситуаций При Эксплуатации ТСВП, Предназначенных Для Эксплуатации На Севере и в Сибири. / С.Д. Попов, С.Н. Чувашев // Сб. Статей Международной Научно-Практической Конференции Инновационное развитие современной науки / ed. А.А. Сукиасян. – Уфа: РИЦ БашГУ, 2014. – Vol. 3. – P. 300-306/366.
9. Попов С.Д. Разработка Технологии Выбора Движительных Комплексов Повышенной Эффективности Для ТСВП, Предназначенных Для Эксплуатации На Севере и в Сибири. / С.Д. Попов, С.Н. Чувашев // Сб. Статей Международной Научно-Практической Конференции Инновационное развитие современной науки / ed. А.А. Сукиасян. – Уфа: РИЦ БашГУ, 2014. – Vol. 3. – P. 296-230/366.
10. Попов С.Д. Отработка Технологий Исследований Составных Частей и Моделей ТСВП, Предназначенных Для Эксплуатации На Севере и в Сибири. / С.Д. Попов, К.В. Долотов, Б.В. Овсянников // Сб. Статей Международной Научно-Практической Конференции Инновационное развитие современной науки / ed. А.А. Сукиасян. – Уфа: РИЦ БашГУ, 2014. – Vol. 3. – P. 281-286/366.
11. Попов С.Д. Амфибийные Транспортные Средства с Гибридным Опорно-Ходовым Комплексом. / С.Д. Попов, А.Е. Дубин // Русский инженер-транспортник (авиация, автомобили, спецтехника). – P. 36-37.
12. Guard U.S.C. Non-standard boat operator’s handbook / U.S.C. Guard. – Washington: U.S. Dept of Transportation, 2006. – 170 p.
13. Баадер Х. Разъездные, Туристические и Спортивные Катера / Х. Баадер. – Л.: Судостроение, 1977. – 382 p.
14. Куликов С.В. Водометные Движители (Теория и Расчет). / С.В. Куликов, М.Ф. Храмкин. – Л.: Судостроение, 1980. – 312 p.
15. Водометный Движитель [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Водомётный_движитель.
16. Алферьев М.Я. Судовые Движители / М.Я. Алферьев. – М.: Мин. Речного флота СССР, 1947. – 662 p.
17. Гребное Колесо – Новый Вариант Мелководного Привода? [Электронный ресурс]. – Режим доступа: http://www.badger.ru/reviews/boats/31077.php.
18. Логвинович Э.Г. Колёсное Судно / Э.Г. Логвинович // Большая Советская Энциклопедия. – М.: Советская энциклопедия, 1969–1978.
19. Мерзляков В.И. Математическая Модель Комплекса Корпус–движитель Судна с Колесными Гребными Движителями / В.И. Мерзляков. – 2012. – № 1. – P. 56-61.
20. Конструкторское Бюро "Возрождение Колесных Судов" [Электронный ресурс]. – Режим доступа: http://www.wheelships.ru/.
21. Якимов Н.М. О Возможности Повышения Эффективности Гребного Колеса При Высокой Скорости Судна : Машиностроение / Н.М. Якимов, С.Д. Попов, С.Н. Чувашев // Вестник Московского государственного технического университета им. Н.Э. Баумана. – 2016. – № 1. – P. 101-111.
22. Якимов Н.М. Выбор Геометрии Эффективного Высокоскоростного Судового Движителя На Основе Гребного Колеса с Учетом Гидроаэродинамики : Машиностроение / Н.М. Якимов, С.Д. Попов, С.Н. Чувашев // Herald of the Bauman Moscow State Technical University. Series Mechanical Engineering. – 2015. – № 6. – P. 50-58.
23. Чувашева Е.С. Комплексная Математическая Модель Для Концептуального Проектирования Высокоскоростных Летательных Аппаратов / Е.С. Чувашева, С.Н. Чувашев, И.Г. Зорина // Информационные технологии. – 2012. – № 11(195). – P. 10-14.
24. Чувашева Е.С. Выбор Рациональных Характеристик Высокоскоростных Летательных Аппаратов Разных Масштабов На Основе Комплексной Математической Модели / Е.С. Чувашева, С.Н. Чувашев // Информационные технологии. – 2013. – № 8. – P. 12-16.
25. Чувашев С.Н. Рабочие Процессы в Узлах Турбокомпрессорного Генератора (Компрессор, Турбина, Электрогенератор) / С.Н. Чувашев, И.Б. Пьянков, Е.С. Чувашева, [et al.]. – Москва: Перо, 2011. – 550 p.
26. Cohen S.D. CVODE, a stiff/nonstiff ODE solver in C / S.D. Cohen, A.C. Hindmarsh // Computers in physics. – 1996. – Vol. 10. – № 2. – P. 138-143.
27. Иванов-Смоленский А.В. Электрические Машины. Vol. 1 / А.В. Иванов-Смоленский. – М.: МЭИ, 2006. – 327 p.
28. Копылов И.П. Электрические Машины / И.П. Копылов. – М.: Энергоатомиздат, 1986. – 360 p.
29. Ландау Л.Д. Курс Теоретической Физики. Учебное Пособие Для ВУЗов : в 10 vols. Vol. 8. Электродинамика сплошных сред / Л.Д. Ландау, Е.М. Лифшиц. – М.: Наука, 1988. – 214 p.
30. Gravdahl J.T. Drive torque actuation in active surge control of centrifugal compressors / J.T. Gravdahl, O. Egeland, S.O. Vatland // Automatica. – 2002. – Vol. 38. – № 11. – P. 1881-1893.
31. Демешко Г.Ф. Проектирование Судов. Амфибийные Суда На Воздушной Подушке Книга 1 / Г.Ф. Демешко. – СПб: Судостроение, 1992. – 269 p.
32. Прохоров А.М. Физический Энциклопедический Словарь / А.М. Прохоров. – М.: Советская энциклопедия, 1983.
33. Справочник По Теории Корабля. Vol. 3. Управляемость водоизмещающих судов. / ed. Я.И. Войткунский. – Л.: Судостроение, 1985.
34. Mantle P.J. Air cushion craft development, first revision / P.J. Mantle. – DAVID W TAYLOR NAVAL SHIP RESEARCH AND DEVELOPMENT CENTER BETHESDA MD, 1980.
35. Шерстюк А.Н. Насосы, Вентиляторы, Компрессоры / А.Н. Шерстюк. – М.: Высшая школа, 1972. – 343 p.
36. Турбины Тепловых и Атомных Электрических Станций / eds. А.Г. Костюк, В.В. Фролов. – М.: МЭИ, 2001. – 488 p.
37. Boyce M.P. Gas turbine engineering handbook / M.P. Boyce. – Amsterdam ; Boston: Elsevier/Butterworth-Heinemann, 2012. – 956 p.
38. Moroz L. A uniform approach to conceptual design of axial turbine / compressor flow path / L. Moroz, Y. Govorushchenko, P. Pagur, [et al.] // Future of Gas Turbine Technology 3 rd International Conference 11-12 October 2006.
39. Kikstra J.F. Dynamic Modeling of a Cogenerating Nuclear Gas Turbine Plant—Part I: Modeling and Validation / J.F. Kikstra, A.H.M. Verkooijen // Journal of Engineering for Gas Turbines and Power. – 2002. – Vol. 124. – Dynamic Modeling of a Cogenerating Nuclear Gas Turbine Plant—Part I. – № 3. – P. 725-733.
40. Абрамович Г.Н. Прикладная Газовая Динамика. Vol. 1 / Г.Н. Абрамович. – М.: Физматгиз, 1991. – 600 p.
41. Абрамович Г.Н. Прикладная Газовая Динамика. Vol. 2 / Г.Н. Абрамович. – М.: Физматгиз, 1991. – 304 p.
42. Черный Г.Г. Газовая Динамика / Г.Г. Черный. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 424 p.
43. Ainley D.G. An Examination of the Flow and Pressure Losses in Blade Rows of Axial-flow Turbines : ARC technical report / D.G. Ainley, G.C.R. Mathieson, A.R.C. Ministry of Supply. – H.M. Stationery Office, 1951.
44. Benner M.W. Influence of Leading-Edge Geometry on Profile Losses in Turbines at Off-Design Incidence: Experimental Results and an Improved Correlation / M.W. Benner, S.A. Sjolander, S.H. Moustapha // Journal of Turbomachinery. – 1997. – Vol. 119. – Influence of Leading-Edge Geometry on Profile Losses in Turbines at Off-Design Incidence. – № 2. – P. 193-200.
45. Александров В.Л. Воздушные Винты / В.Л. Александров. – М.: Оборонгиз, 1951.
46. Кравец А.С. Характеристики Воздушных Винтов / А.С. Кравец. – М.: Оборонгиз, 1941.
47. Ветчинкин В.П. Теория и Расчет Воздушного Гребного Винта / В.П. Ветчинкин, Н.Н. Поляков. – М.: Оборонгиз, 1940.
48. Шайдаков В.И. Аэродинамическое Проектирование Лопастей Воздушного Винта / В.И. Шайдаков, А.Д. Маслов. – М.: МАИ, 1995. – 34 p.
49. Шайдаков В.И. Аэродинамический Расчет Вертолета / В.И. Шайдаков. – М.: МАИ, 1988.
50. Юрьев Б.Н. Аэродинамический Расчет Вертолета / Б.Н. Юрьев. – М.: Оборонгиз, 1956.
51. Larrabee E.E. The screw propeller / E.E. Larrabee // Scientific American. – 1980. – Vol. 243. – P. 134.
52. Hughes M.J. Analysis of Multi-component Ducted Propulsors in Unsteady Flow / M.J. Hughes. – Massachusetts Institute of Technology, 1993.
53. Ardito Marretta R.M. Hybrid numerical technique for evaluating wing aerodynamic loading with propeller interference / R.M. Ardito Marretta, G. Davi, G. Lombardi, [et al.] // Computers & Fluids. – 1999. – Vol. 28. – № 8. – P. 923-950.
54. Molland A.F. The maritime engineering reference book a guide to ship design, construction and operation / A.F. Molland. – Amsterdam; Boston; London: Butterworth-Heinemann, 2008.
55. Остославский И.В. Характеристики Винтовых Профилей Типа Кларк-У / И.В. Остославский, Д.В. Халезов // Технические заметки ЦАГИ. – 1937. – № 154.
56. Кашафутдинов С.Т. Атлас Аэродинамических Характеристик Крыловых Профилей / С.Т. Кашафутдинов, В.Н. Лушин. – Новосибирск: СибНИА, 1994. – 78 p.
57. Hindmarsh A.C. The PVODE and IDA algorithms / A.C. Hindmarsh. – Technical Report UCRL-ID-141558, LLNL, 2000.
58. Inc. A. ANSYS CFX-Solver Theory Guide / A. Inc. // Ansys CFX release 14 Help System. – 2012.
59. Колесный Движитель.
60. Denery T. Multi-Domain Modeling of the Dynamics of a Hovercraft for Controller Development / T. Denery // AIAA Modeling and Simulation Technologies Conference and Exhibit : Guidance, navigation, and control and co-located conferences. – American Institute of Aeronautics and Astronautics, 2005.
61. Прохоров А.М. Физическая Энциклопедия. Vol. 5 / А.М. Прохоров. – М.: Большая Российская энциклопедия, 1998.
62. Кошкин Н.И. Механика. Динамика Вращательного Движения / Н.И. Кошкин // Элементарная Физика: Справочник. – М.: Наука. Гл. ред. физ.-мат. лит.,. – P. 32.
63. Witkin A. Physically Based Modeling: Principles and Practice – Constrained Dynamics / A. Witkin // COMPUTER GRAPHICS. – 1997. – Physically Based Modeling. – P. 11-21.
64. Якимов Н.М. Программное Средство Для Комплексного Математического Моделирования Сложных Технических Объектов / Н.М. Якимов, С.Н. Чувашев // ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ. – 2014. – № 11. – P. 23-30.
65. Pierson W.J. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii / W.J. Pierson, L. Moskowitz // Journal of Geophysical Research. – 1964. – Vol. 69. – № 24. – P. 5181-5190.