Введение
Быстрый рост вычислительной мощности ЭВМ в последние десятилетия делает возможным использование компьютерного математического моделирования для все более сложных объектов. Использование математического моделирования позволяет избежать многократного использования прототипов и, при правильном подходе, позволяет сократить стоимость разработки концептуально новых решений и продуктов.
При моделировании сложных технических объектов важной оказывается возможность изолированного исследования подсистем, составляющих данный объект. Это связано как с необходимостью верификации построенных математических моделей, отладки построенных программных комплексов, так и с необходимостью решения задач различных дисциплин в различных подсистемах. Изолированное исследование подсистем технически сложного объекта позволяет, с одной стороны, верифицировать и отлаживать более простые системы, и затем идти от простого к сложному, а с другой стороны, упрощает разработку, параллельно ведущуюся различными группами исследователей. Модель объекта, составленную из моделей подсистем, можно представить, как некий комплекс моделей, или комплексную модель. Дополнительным преимуществом использования комплексных моделей является возможность повторного использования уже разработанных моделей подсистем для использования в комплексных моделях других объектов, т.е. использования некой библиотеки моделей при разработке.
При моделировании технически сложных объектов возникают вычислительные задачи большой размерности, для решения которых оказывается необходимо применять различные специализированные математические методы. Для уменьшения размерности задачи могут использоваться также подходы иерархического моделирования и табличного задания процессов с использованием экспериментальных или модельных результатов.
Использование библиотеки моделей накладывает требование возможности быстрой адаптации библиотечных моделей под условия разрабатываемой.
На основе вышесказанного, а также нашего многолетнего опыта разработки комплексных моделей различных объектов (космических энергоустановок [1], гиперзвуковых летательных аппаратов [2; 3], судов на воздушной подушке [4] и др.) можно сформировать следующие требования для программного комплекса, решающего задачу комплексного моделирования:
Автоматическая сборка комплексной модели из моделей подсистем
Возможность использования различных численных методик для решения задач высокой размерности (в т.ч. поддержка пользовательских компонентов-решателей)
Поддержка подходов иерархического моделирования и табличного задания процессов
Возможность быстрой корректировки библиотечных моделей под изменяющиеся требования
С точки зрения удобства использования программного пакета, можно сформулировать несколько дополнительных требований:
Графическое редактирование связей между моделями подсистем
Использование стандартного языка для разработки моделей
Низкая стоимость лицензии на одно рабочее место
Графическое редактирование является наиболее наглядным представлением, что дает более высокую устойчивость к ошибкам. Использование стандартного языка уменьшает порог вхождения и затраты на обучение. Последнее требование продиктовано необходимостью возможности параллельной разработки различными группами исследователей: при высокой стоимости лицензии на рабочее место, необходимы либо крупные капиталовложения для обеспечения каждой группы, либо дополнительные программные и технические средства для обеспечения параллельного или удаленного доступа к программному комплексу.
Анализ существующих решений
На текущий момент на рынке программного обеспечения существует ряд решений для блочного и компонентного моделирования систем. Многие из этих решений на данный момент активно развиваются. Тем не менее, большинство из существующих решений оптимизировано под определенные классы задач, в связи с чем их применение к более широкому кругу проблем оказывается осложнено.
Наиболее известными сейчас являются решения для блочного моделирования, такие как Matlab Simulink[???], VisSim[???], и их открытые аналоги, такие как Scicos[???]. Общей проблемой подобных решений является их ориентированность на разработку моделей для обработки сигналов, в частности электрических и гидравлических цепей. Несмотря на то, что для подобных применений эти решения подходят достаточно хорошо, для реализации более сложных моделей требуются значительные усилия[???].
Другой проблемой этих систем является часто жестко заданный набор решателей дифференциальных уравнений. В случае систем с открытым исходным кодом эта проблема стоит не столь остро, однако, если поставляемые решения не удовлетворяют требования решаемой задачи, добавление пользовательских решателей в открытые системы оказывается сопряжено с большим количеством работы по освоению существующей кодовой базы [???].
Сравнительно новой альтернативой подходу блочного моделирования является компонентное моделирование систем. К программным решениям этого класса относятся, например, EcosimPro[???], ASCEND[???], EMSO[???] и различные реализации стандарта Modelica[???], как открытые, например, OpenModelica[???] и JModelica[???], так и проприетарные, например, Dymola[???], MapleSim[???], AMESim[???] и др.
Все перечисленные решения для компонентного моделирования обладают общей проблемой: адаптация старых исходных кодов моделей на Fortran, C или C++ требует генерации специальным образом сформированной динамической библиотеки (DLL или SO) либо специальным образом сформированного исходного кода (в случае AMESim).
Другой проблемой, вытекающей из предыдущей, является необходимость освоения собственного скриптового языка данной системы. При этом, даже решения на основе Modelica обладают присущими только им особенностями языка, которые необходимо знать для эффективного использования этих решений.
Подключение сторонних решателей и/или интеграторов, как и в случае с решениями для блочного моделирования, также поддерживается не всеми перечисленными программными пакетами. Подробная документация приведена только для ASCEND (в котором на момент написания эта функциональность является экспериментальной) и EMSO.
К недостаткам закрытых решений также можно отнести их высокую стоимость, так, например, Dymola (не продается в России) оценивается в $5000 для полной редакции ($1200 для упрощенной), а дополнительные компоненты, такие, как 3D-визуализация, дополнительно увеличивают стоимость на $1200-1500. AMESim оценивается в $11000, MapleSim – около $7000. Все цены приведены для лицензий на одного пользователя.
Что касается открытых решений, ASCEND, несмотря на длительное присутствие на рынке, на момент написания значительно проигрывает другим программным пакетам по функциональности (которая либо не реализована, либо является экспериментальной). Это позволяет предположить, что разработка ведется крайне медленными темпами. Подобное заключение можно сделать и о “полузакрытом” EMSO, активная разработка которого не ведется с 2010 года, а многие цели, которые планировалось реализовать еще к 2008 году, не реализованы до сих пор. К тому же, по условиям лицензии, основной программный пакет EMSO доступен только для образовательных и некоммерческих применений.
JModelica, несмотря на активную разработку, на момент написания реализует стандарт Modelica только частично[???], поэтому использование может быть дополнительно осложнено.
Более полное сравнение программных продуктов приведено в табл. 1.
Предлагаемое программное решение
Из вышесказанного следует, что использование существующих программных продуктов для создания и анализа комплексных моделей не всегда удобно. В связи с этим, был разработан новый программный пакет, смягчающий многие из перечисленных недостатков.
Автоматическая сборка комплексной модели из моделей подсистем обеспечивается модулем “компилятора”, принимающим на вход файл-описание и исходные коды и создающим двоичный исполняемый файл комплексной модели, который затем можно использовать отдельно от программного комплекса. Модуль “компилятора” написан с использованием C++ и пакета библиотек Boost.
Модульная архитектура позволяет использование пользовательских интеграторов и решателей. Стандартный API требует от модуля решателя только использования соглашений на именование и прототипы функций и использование XML фиксированного формата для управления настройками решателя и модели.
Использование полного С++ в качестве языка описания моделей позволяет легко вставлять в модели таблично задаваемые параметры с использованием любого метода интерполяции.
Адаптация “старых” моделей как правило сводится к написанию простого “адаптера”, описывающего входы и выходы, и небольшой модификации исходной модели для работы с “адаптером”.
Библиотечные модели целиком копируются в проект, поэтому их изменение в рамках проекта не требует дополнительных действий. Возможна модификация моделей на этапе связывания в комплексную модель.
Инструмент графического редактирования связей между моделями подсистем написан на С++ с использованием графических библиотек Qt.
Все основные инструменты программного пакета написаны на C++ с использованием кроссплатформенных библиотек, что позволяет легко переносить программный пакет на любую платформу с поддержкой этих библиотек, в частности, на Linux, Windows и Mac OSX.
Структура комплексной модели
Математическую модель можно представить, как некую систему уравнений. Система уравнений характеризуется, в свою очередь, переменными, значения которых могут быть постоянны, либо изменяются дискретно или непрерывно, и уравнениями, описывающими связь этих переменных между собой. Для разрешимости задачи математического моделирования необходимо, чтобы система, описывающая данную модель, была замкнутой. Соответственно, если исходная система не замкнута, для введения дополнительных условий оказывается необходимо добавить к исходной еще одну или несколько систем уравнений, описывающих поведение неопределенных в исходной системе переменных. Рассуждая таким образом, можно предложить следующую схему представления моделей подсистем: моделью подсистемы (“простой” моделью) является некоторая система уравнений, имеющая N неопределенных переменных, где N≥0. Совокупность простых моделей можно считать комплексной моделью, причем комплексная модель так же может быть незамкнутой. Окончательно, комплексная модель, пригодная для моделирования, может представлять из себя такую совокупность простых и комплексных моделей, в которой все переменные определены. Переменные, определенные в рамках данной модели, мы будем называть “выходными параметрами”. Переменные, не определенные в рамках данной модели, будем называть “входными параметрами”.
Для описания комплексной модели используется иерархическое дерево: простые модели, описываемые при помощи исходного кода на языке C++ и файла XML с описанием входных и выходных параметров, являются “листьями” этого дерева. “Листья” объединяются в ветви, сами представляющие из себя комплексные модели. Комплексные модели должны дополнительно описывать связи параметров между входящими в них моделями. Наконец, “корнем” дерева является комплексная модель, состоящая из простых и комплексных моделей, в которой все входные параметры определены. Все дерево далее будем называть “проектом”.
В качестве формата файлов проекта выбраны zip-файлы со сжатием deflate, содержащие исходные коды входящих в проект моделей и XML-файл описания, содержащий информацию о входных и выходных параметрах моделей (в т.ч. название, описание, размерность, и т.п.), а также о связях между параметрами и исходном коде. Кроме того, отдельные модели при необходимости сохраняются в аналогичных по структуре zip-файлах и могут быть впоследствии загружены в другой проект.
Модуль “компилятора”
Модуль компилятора преобразует файлы проекта в бинарные исполняемые файлы модели, пригодные для расчетов. Этот процесс происходит в несколько этапов:
Строится граф зависимостей всех параметров модели
Проверяется наличие циклических зависимостей
Исходные коды моделей переписываются в вид, пригодный для использования с модулями решателей
Определяется порядок расчета параметров комплексной модели на основе топологической сортировки
Генерируется функция состояния системы, пригодная для использования с модулями решателей
Полученные коды компилируются и линкуются с решателем при помощи внешнего компилятора С++
Генерируется файл настроек
Граф зависимостей параметров строится на основе синтаксического анализа исходных кодов моделей и связей, указанных в XML-описании проекта. Для проведения синтаксического анализа используются регулярные выражения (библиотека Boost Xpressive).
Поиск циклических зависимостей и топологическая сортировка производятся стандартными алгоритмами.
На третьем этапе все параметры линеаризуются, т.е. представляются в виде массива скаляров, и соответствующие именованные параметры моделей заменяются на внутреннее представление. Кроме этого, во избежание конфликта имен функций, функции моделей переименовываются уникальным образом (добавлением префикса, характеризующего положение модели в иерархии проекта). Входные и выходные параметры, связанные равенством, используют одну ячейку памяти, однако с разным спецификатором доступа: изменение входных параметров запрещено.
Функция состояния системы для случая моделей, описываемых системами ОДУ, возвращает правую часть задачи Коши. Для случая систем ДАУ или алгебраических уравнений – вектор остаточных членов системы.
Файл настроек представляет из себя файл XML, содержащий информацию о начальных значениях параметров, задаваемых дифференциальными уравнениями, значениях параметров, обозначенных как постоянные, и настройках модуля решателя.
Инструмент графического редактирования связей
Инструмент графического редактирования связей предназначен для связывания отдельных “простых” моделей в комплексную. Модель графически представляется в виде прямоугольника с выходящими из его ребер линиями с квадратом на конце (далее “блок”), отражающими входные и выходные параметры модели (далее “коннекторы”). При этом, “входные” коннекторы (для входных параметров) расположены на правой грани, “интегрируемые” – на верхней, постоянные – на нижней и “выходные” – на правой (рис. 1, 2)
Методом “drag&drop” возможно связывание всех прочих коннекторов с входными. Для упрощения визуального восприятия, коннекторы автоматически кодируются цветом. Цвета связующей линии и входного коннектора соответствуют цвету связанного выходного коннектора. Возможно связывание одного выходного коннектора с несколькими входными, но не наоборот.
Также возможно создание блоков комплексных моделей, включающих в себя несколько “простых” или других комплексных моделей, как полностью определенных, так и частично. При этом неопределенные в рамках такого блока параметры должны быть “экспортированы” (экспорт реализуется пунктом контекстного меню коннектора). На блоке комплексной модели отображаются только коннекторы “экспортированных” параметров. Блок комплексной модели можно “развернуть” двойным кликом на нем.
Любой блок может быть сохранен в виде файла модели. Так же любой ранее сохраненный блок возможно загрузить в новую модель.
Кроме того, инструмент графического редактирования связей включает в себя возможности для редактирования исходного кода моделей, добавления или удаления параметров и возможности создания новых моделей в процессе работы.
Модуль решателя
Модуль решателя представляет из себя статическую библиотеку со строго определенным API. Строго говоря, API определяет всего одну функцию solve с одним параметром – экземпляром вспомогательного класса, предоставляющим информацию о времени счета, времени остановки, настройках решателя, а также вспомогательные функции, реализующие инициализацию, вывод и расчет правых частей задачи Коши.
На текущий момент реализованы следующие решатели:
Решатель DOPRI5[???] (адаптирован из старого кода на языке FORTRAN)
Решатель RADAU5[???] (адаптирован из старого кода на языке FORTRAN)
Решатель SUNDIALS CVODE[5] (написан интерфейс, “стыкующий” библиотеки SUNDIALS с API решателя)
Инструмент анализа решения
Инструмент анализа решения позволяет изменять начальные условия и постоянные без повторной сборки модели. Кроме того, графически отображает решение, позволяет сохранять и конвертировать файл решения в различные форматы (на текущий момент ascii-таблица и tecplot).
Формат решения предполагает текстовое описание, которое также вводится из интерфейса данного инструмента.
В процессе решения, графики периодически обновляются (рис. 3). Так же отображается общий прогресс решения.
Возможен многопараметрический анализ, реализуемый многократным расчетом модели (рис. 4)
Пример использования
Рассматривается пример использования предлагаемого программного средства для моделирования технически сложных объектов на примере мельницы для измельчения твердых органических материалов. С одной стороны, подобное устройство годится как пример системы, принцип действия которой знаком из бытовой техники, с другой стороны, его моделирование и оптимизация потребовались, в частности, для решения задачи экономически эффективного получения микронных порошков органического сырья, критически важной для масштабной программы получения биотоплива.
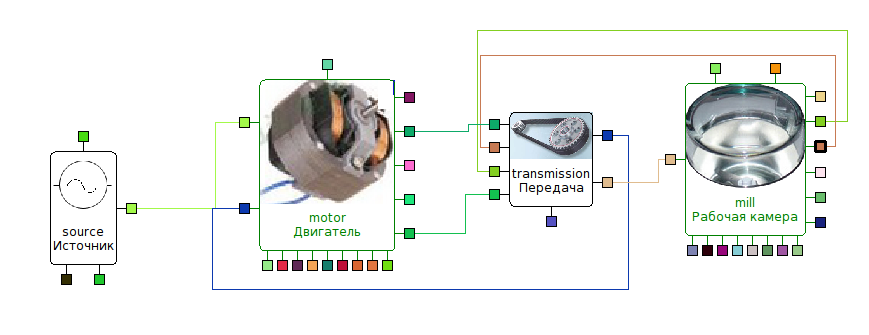
Структурная схема комплексной модели показана на рис. 1. Комплексная модель мельницы состоит из блоков:
Модель асинхронного однофазного электрического двигателя
Модель ременной передачи
Модель источника синусообразного тока
Модель рабочей камеры
Модель электрического двигателя разработана в нашей работе [1] на основе [6; 7]. В модели учтены эффекты влияния ширины зазора, взаимовлияние катушек ротора и статора, индуктивности рассеяния катушек, описывается динамика раскрутки и торможения ротора, динамические эффекты на стартовом конденсаторе. Оценивается стоимость двигателя (пропорционально объему материалов, требуемых для его изготовления, что верно при массовом производстве).
Модель помола построена на основе предположения, что обмен импульсоммежду частицами эффективен, т.е. что частицы движутся с минимальнымискоростями относительно друг друга. Тогда скорость частиц \(v\) направленатангенциально, причем её модуль пропорционален радиальному размеру \(r\):
\[v = \omega r.\]
Частота вращения ω определяется уравнением баланса моментов для вращения [8].
\[J \frac{\partial\omega}{\partial t} = M_i - M_w.\]
Здесь \(J\) − момент инерции, \(t\) − время, \(M_i\) − вращательный момент отударного взаимодействия частиц с ножом, \(M_w\) − вращательный момент оттрения частиц о стенку. Для цилиндрической засыпки
\[J = \int_0^R\rho r^2 dV = \int_0^R \rho r^2 h 2\pi r dr = \frac{1}{2}\pi\rho h R^4,\]
здесь \(V\)− объём, \(h\) − высота, \(\rho\) − плотность засыпки, \(\rho\) = \(C_\rho \rho_0\),\(C_\rho\) − объёмная доля твердого материала, для сферических частиц \(C_\rho=\pi/6\), \(\rho_0\) − плотность твердого материала, \(R\) − радиальный размеркамеры. При трении частиц о стенку тормозящий момент
\[M_w = C_w p_w (2\pi R h) R,\]
здесь \(C_w\) − коэффициент трения, \(p_w\) − давление на стенку, для цилиндрической засыпки
\[p_w = \int_0^R a\rho dr = \int_0^R r\omega^2 \rho dr = R^2 \omega^2 \rho.\]
Здесь \(a\) − ускорение. Вращательный момент от ударного взаимодействиячастиц с двумя ножами
\[ M_i = 2 R_k \nu_k (C_k+1) 2 m (v_k - v_m) = \] \[ 2 R_k (C_k+1) 2\rho h_k \delta_k (R_k\Omega - R_k\omega)^2 = \] \[ 4(C_k+1) R_k^3 \rho h_k \delta_k (\Omega-\omega)^2,\]
здесь \(R_k\) − радиальная координата рабочей поверхности ножа, \(h_k\) −её высота, \(\delta_k\) − толщина, \(m\) − масса частицы, \(\nu_k\) − частота соударений, \(v_k\) − скорость ножа, \(v_m\) − скорость частицы досоударения, \(\Omega\) − частота вращения ножа, \(C_k\) − коэффициент упругости удара, \(C_k = 1\) для абсолютно упругого и \(C_k = 0\) для абсолютно неупругого удара.
Помол при высокоскоростном ударе рассчитывался из уравнения [???]
\[\frac{\partial N_p(t)}{\partial t} = N_{p0} K \frac{v_{rel}^2}{\sqrt{x_p}}\]
здесь \(v_{rel}\) − относительная скорость столкновения частицы и ножа, \(t\) − время, \(N_p(t)\) − текущее, \(N_{p0}\) − начальное число частиц, \(x_p\) − текущий средний характерный размер частиц, связанный с \(N(t)\), \(K\) − коэффициент, определяемый механическими свойствами обрабатываемого материала.
Каждый из блоков разрабатывался и тестировался отдельно. Полные исходные коды модели составляют 170 строк. Исходные коды, сгенерированные компилятором, составляют 809 строк.
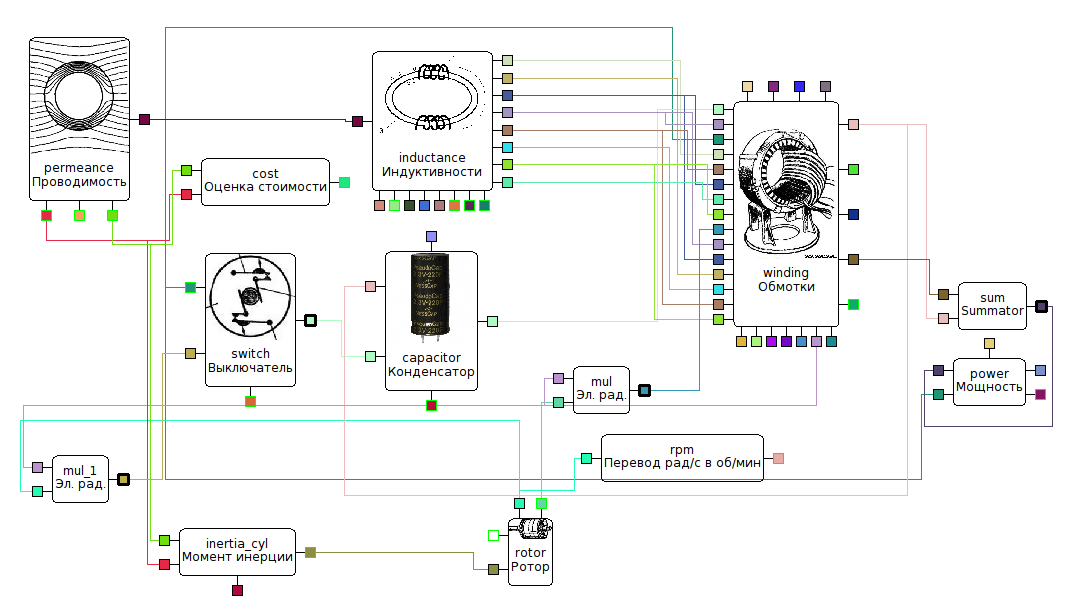
На рис. 2 показана структурная схема комплексной модели электрического двигателя. Модель двигателя можно изолированно использовать, например, для анализа раскрутки ротора в режиме холостого хода. Так, например, при увеличении момента инерции ротора (за счет увеличения радиуса), время раскрутки увеличивается (рис. 3).
При использовании модели электродвигателя в составе модели мельницы отдельные модели автоматически объединяются в общий комплекс. С помощью этого комплекса можно проводить анализ и оптимизацию различных характерных параметров конструкции и режимов, например, в терминах стоимость-производительность. Под производительностью понимается масса измельченного материала, отнесенная ко времени измельчения.
В качестве примера, рассмотрим задачу оптимизации соотношения производительность/стоимость по параметру размера рабочей камеры. Проводится несколько серий расчетов работы мельницы при пропорциональном изменении размеров элементов двигателя. Для каждого набора параметров определяется время достижения необходимого размера частиц (300 мкм). По заданной массе материала определяется производительность. По геометрическим параметрам определяется стоимость. Строится график производительности от стоимости для различных размеров рабочей камеры (рис. 4).
С помощью комплексной модели данного технически сложного объекта продемонстрирована принципиальная возможность использования ее на стадии эскизного проектирования мельницы с целью повышения качества проектирования и снижения издержек на разработку. При этом моделируются аспекты различных рабочих процессов, преодолеваются трудности, связанные с различными пространственными и временными масштабами рабочих процессов в различных подсистемах. Продемонстрирована принципиальная возможность проведения многопараметрического анализа на этапе эскизного проектирования. Показано значительное уменьшение объема необходимого исходного кода (по крайней мере, в 4 раза).
Заключение
Разработано программное обеспечение, которое, по-видимому, лучше других удовлетворяет комплексу требований для математического моделирования технически сложных объектов, состоящих из подсистем, рабочие процессы в которых относятся к различным областям знаний и моделируются различными автономными группами исследователей с различной степенью подробности (в т.ч. с использованием подходов иерархического моделирования и табличного задания процессов). Язык разработки автономных моделей подсистем общеизвестный – C++, переносимый на большинство популярных платформ, что снижает порог вхождения новых групп исследователей.
| Simulink | VisSim | Scicos | EcosimPro | ASCEND | EMSO | OpenModelica | JModelica | Dymola | SM1 | MapleSim | AmeSim | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | + | + | + | + | + | + | + | - | + | + | + | + |
| 2 | - | + | * | - | + | + | * | * | - | - | - | - |
| 3 | - | - | * | - | + | + | * | * | - | - | - | - |
| 4 | † | † | † | † | † | † | † | † | † | + | + | + |
| 5 | † | † | † | + | + | + | † | - | + | † | † | + |
| 6 | - | - | - | - | - | - | ‡ | ‡ | ‡ | ‡ | ‡ | + |
| 7 | - | - | - | + | + | + | + | + | + | + | + | + |
| 8 | + | + | + | + | - | + | + | - | + | + | + | + |
| 9 | W,L,M | W | W,L,M | W | W,L | W,L | W,L,M | W,L,M | W,L | W,M | W,L,M | W,L |
| 10 | $5000 | $3840 | Беспл. | $1500-2500 | Беспл. | Некомм. | Беспл. | Беспл. | $5000 | $2450 | $7000 | $11000 |
1. Автоматическая сборка комплексной модели из моделей подсистем. 2. Пользовательские решатели. 3. Пользовательские интеграторы. 4. Табличное задание процессов/параметров .5. Сравнительно легкая адаптация “старых” моделей на компилируемых языках (Fortran, C, etc). 6. Использование стандартного языка для разработки моделей. 7. Быстрая корректировка библиотечных моделей. 8. Графическое редактирование связей между моделями подсистем. 9. Поддерживаемые ОС (W – Windows, L – Linux, M – Mac OSX). 10. Примерная стоимость лицензии на рабочее место
* – функция теоретически доступна, но не поддерживается. Требуется редактирование исходного кода или дополнительные технические приемы.
† – функция, реализуемая посредством сложных манипуляций другими возможностями программы
‡ – использование узко специфичного языка Modelica
Список иллюстраций


Список литературы
1. Чувашев С.Н. Рабочие Процессы в Узлах Турбокомпрессорного Генератора (Компрессор, Турбина, Электрогенератор) / С.Н. Чувашев, И.Б. Пьянков, Е.С. Чувашева, [et al.]. – Москва: Перо, 2011. – 550 p.
2. Чувашева Е.С. Комплексная Математическая Модель Для Концептуального Проектирования Высокоскоростных Летательных Аппаратов / Е.С. Чувашева, С.Н. Чувашев, И.Г. Зорина // Информационные технологии. – 2012. – № 11(195). – P. 10-14.
3. Чувашева Е.С. Выбор Рациональных Характеристик Высокоскоростных Летательных Аппаратов Разных Масштабов На Основе Комплексной Математической Модели / Е.С. Чувашева, С.Н. Чувашев // Информационные технологии. – 2013. – № 8. – P. 12-16.
4. Попов С.Д. Разработка Технологии Выбора Несущего Комплекса Для Транспортных Средств На Воздушной Подушке (ТСВП), Предназначенных Для Эксплуатации На Севере и в Сибири / С.Д. Попов, С.Н. Чувашев // Сб. Статей Международной Научно-Практической Конференции Инновационное развитие современной науки / ed. А.А. Сукиасян. – Уфа: РИЦ БашГУ, 2014. – Vol. 3. – P. 287-295.
5. Cohen S.D. CVODE, a stiff/nonstiff ODE solver in C / S.D. Cohen, A.C. Hindmarsh // Computers in physics. – 1996. – Vol. 10. – № 2. – P. 138-143.
6. Иванов-Смоленский А.В. Электрические Машины. Vol. 1 / А.В. Иванов-Смоленский. – М.: МЭИ, 2006. – 327 p.
7. Копылов И.П. Электрические Машины / И.П. Копылов. – М.: Энергоатомиздат, 1986. – 360 p.
8. Ландау Л.Д. Курс Теоретической Физики. Учебное Пособие Для ВУЗов : в 10 vols. Vol. 8. Электродинамика сплошных сред / Л.Д. Ландау, Е.М. Лифшиц. – М.: Наука, 1988. – 214 p.