Введение

Для решения ряда задач представляют интерес первые секунды динамики образования после попадания в высокоскоростной дозвуковой поток воздуха облачков из протяжённых электропроводных элементов – диполей, и их взаимодействия с поляризованным радиоизлучением, длина полуволны которого одного порядка величины с длинами диполей.

Описание взаимодействия диполя с электромагнитной волной давно известно. Теоретическому описанию взаимодействия облачков диполей с радиоизлучением также посвящена достаточно обширная литература [1]. Однако, судя по доступным данным, указанная выше задача до сих пор не решена в отношении адекватного описания в комплексе всех соответствующих процессов: инжекции плотного компакта диполей, их разделения, дальнейшего разлёта, взаимодействия с воздушной средой, взаимодействия с радиоизлучением данной поляризации с учётом неоднородного пространственного распределения и анизотропии расположения диполей, многократного рассеяния, и др. Как правило, ранее подробно анализировались отдельные аспекты, а вместо описания других применялись упрощающие приближения, например, изотропной ориентации диполей, их равномерного или случайного расположения в объёме наперёд заданной формы (шаровое или кубическое облако), точно поперечного расположения в потоке и т.д. [1–5]. Часто для оценок применяется формула для суммарного сечения обратного рассеяния \(\sigma_{\Sigma\mathrm{max}}\) в простом частном случае – при совпадении длины полуволны излучения и длины диполей (резонансное излучение), оптической прозрачности облака и хаотической ориентации диполей [6]: \[ \sigma_{\Sigma \mathrm{max}} \approx 0.15 \lambda^2 N,\qquad(1)\] где \(\lambda\) – длина волны резонансного излучения, \(N\) – число диполей. Но практически все указанные предположения не выполняются в рассматриваемом случае. Требуется, очевидно, более подробное рассмотрение. Этому посвящена данная работа.

1 Методика расчёта динамики и взаимодействия с излучением облаков диполей

1.1 Методика расчёта начальной стадии разлёта компакта диполей

В течение начальной стадии после попадания цилиндрического компакта диполей в поток воздуха, плотность компакта значительно превосходит плотность воздуха. Сечение рассеяния излучения ещё мало, эта стадия короткая, она интересна только с точки зрения нахождения начальных условий для следующей, основной стадии, когда средняя плотность облака диполей меньше плотности вмещающего воздуха. Поэтому, вместо моделирования движения в возмущённом потоке многочисленных тел, рассматривается обтекание компакта диполей как жидкого тела с нулевым поверхностным натяжением. При этом формируется максимум давления перед ним и зона минимального давления по периферийным границам, наиболее удалённым от оси, направленной по потоку [7]. Под действием этих перепадов давления, занятый диполями объём деформируется, увеличивая радиальные размеры. На передней границе имеются также условия развития неустойчивости Релея-Тейлора. На начальных стадиях этого процесса расширение нормального к скорости потока диаметра \(D\) объёма диполей \(V\) описывается уравнением [7] \[ \frac{\partial D}{\partial t} = D \sqrt{ \frac{4\pi^2 v^2 \rho_a \rho_V} {D^2 \left({\rho_a+\rho_V}\right)^2} + \frac{2\pi \dot{v}\left({\rho_V-\rho_a}\right)} {D\left({\rho_V+\rho_a}\right)} } \qquad(2)\] здесь \(\rho_V\) – плотность жидкого объёма \(V\) (в нашем случае – суммарная масса диполей \(M\), отнесённая к объёму), \(\rho_a\) – плотность воздуха, \(\dot{v}\) – ускорение. Первый член выражения для квадрата инкремента учитывает работу сил давления, второй – неустойчивость Релея-Тейлора.

Скорость \(v\) центра масс жидкого объёма относительно воздуха определяется уравнением Ньютона с учётом аэродинамического сопротивления \[ M \frac{\partial v}{\partial t} = - C_x \frac{1}{2} \rho_a v^2 \cdot \frac{1}{4} \pi D^2 \qquad(3)\] Здесь \(C_x \approx 1\) – коэффициент аэродинамического сопротивления.

Уравнения (2, 3) решалась численно для различных диполей и скоростей инжекции \(v_i = v(t=0)\) до снижения плотности \(\rho_V\) до уровня \(\rho_a\). Отметим, что это соответствует увеличению диаметра квазисферического облака в \(13\ldots 20\) раз. Результаты вычислений при начальных скоростях компакта \(50\ldots 200\) м/с показали, что, например, 10 г примерно миллиона диполей с основой из стекловолокна, покрытого хорошо проводящим слоем металла, разлетаются до смены режима за \(1\ldots 5\) мс, а 35-граммовый компакт диполей из стальной проволоки – за несколько большее время – \(2.5\ldots 9\) мс (большие времена соответствуют меньшим начальным скоростям). При этом скорость облака диполей снижается на \(\approx 15\%\), и появляется радиальная составляющая, соответствующая полууглу разлёта \(15\ldots 35 {^\circ}\).

1.2 Методика расчёта движения диполей в воздухе

Из вышеуказанного следует, что достаточно быстро, за несколько миллисекунд после момента инжекции заряда, плотность облака диполей \(\rho_d\) становится меньше плотности воздуха \(\rho_a\). Переход от \(\rho_d \gg \rho_a\) к \(\rho_d \ll \rho_a\) весьма быстрый, т.к. облако диполей в этот период быстро расширяется, поэтому неучёт особенностей стадии, когда \(\rho_d \approx \rho_a\) и движения диполей и воздуха влияют друг на друга, не меняет заметным образом дальнейшую динамику диполей. Т.о, с момента выравнивания плотностей можно пренебречь возмущением воздуха от инжекции и рассматривать отдельно полёт каждого из диполей.

Приготовленные для дальнейших исследований диполи с основой из стекловолокна, покрытого слоем металла, как оказалось, не являются точно прямолинейными, имеются небольшие нерегулярные искривления; как показано ниже, это влияет на результаты. Для учёта отклонения формы диполя от кругового цилиндра он считается состоящим из нескольких цилиндрических частей, соединённых друг с другом. Осевая линия диполя рассматривается как плоская ломаная из одинаковых по длине отрезков – осей цилиндров. Форма диполя определяется углами наклона каждого отрезка ломаной к некоторой прямой, которые задаются случайными числами от 0 до \(\zeta_\mathrm{max}\).

Динамика полёта диполей рассчитывалась по дифференциальным уравнениям динамики сложного движения трёхмерного твёрдого тела [8]: \[m\frac{\partial\vec{v}}{\partial t} = \vec{R}+\vec{G}\] \[\vec{G} = - m \vec{g}\] \[I_{x'} \frac{\partial\omega_{x'}}{\partial t}{t} + (I_{z'}-I_{y'})\omega_{y'}\omega_{z'} = M^R_{x'}\] \[I_{y'} \frac{\partial\omega_{y'}}{\partial t}{t} + (I_{x'}-I_{z'})\omega_{x'}\omega_{z'} = M^R_{y'}\] \[I_{z'} \frac{\partial\omega_{z'}}{\partial t}{t} + (I_{y'}-I_{x'})\omega_{y'}\omega_{x'} = M^R_{z'}\] здесь \(m\) – масса, \(t\) – время, \(x',y',z'\) – координаты, связанные с диполем и направленные по его главным осям инерции, \(x,y,z\) – координаты, связанные с Землёй, индексы обозначают проекции на соответствующие оси, \(\vec{v}\) – скорость, \(\vec{\omega}\) – угловая скорость, \(\vec{R}\) – сила аэродинамического сопротивления, \(\vec{g}\) – ускорение свободного падения, \(\vec{M^R}\) – вращательные моменты, \(I_{x',y',z'}\) – моменты инерции вдоль главных осей. Аэродинамические силы, действующие на диполь, рассчитывались отдельно для каждой части диполя как для длинного цилиндра, обдуваемого под соответствующим углом атаки, в соответствии с полуэмпирическими зависимостями [9–11] с учётом изменения относительных локальных скоростей воздуха и чисел Рейнольдса из-за вращения диполя. Моменты рассчитывались интегрированием сил и соответствующих плеч по длине диполя. При расчёте моментов инерции учитывалось, что диполь имеет малую, но конечную толщину.

1.3 Методика подробного расчёта взаимодействия ансамбля диполей с электромагнитным излучением

Взаимодействие диполей с излучением рассматривается как рассеяние плоской электромагнитной волны на системе бесконечно проводящих тел. На всех границах задаются условия свободного выхода излучения из расчётного объёма.

Принимаются приближения, справедливые при радиусе \(a\) проводника много меньше и длины проводника, и длины волны \(\lambda\):

1. Токи в проводнике ограничены поверхностью
2. Проводник состоит из частей, которые имеют цилиндрическую форму
3. Используется приближение тонкого провода в ослабленной формулировке [12]:
   1. Поперечные токи в части проводника пренебрежимо малы по сравнению с продольными
   2. Изменение продольного тока по радиусу может не учитываться
   3. Ток может быть представлен как ток вдоль нити конечной толщины, расположенной на оси части проводника
   4. Граничное условие для электрического поля должно принудительно применяться только в продольном направлении.

Для решения этой задачи используется метод [13], сводящийся в данном случае к решению уравнения: \[- \hat{s}(\vec{r}) \times {\vec{E^I}}(\vec{r}) = \frac{- i\eta}{4\pi k}\int_{L}^{}I(s') \cdot \left( k^{2}\hat{s}' - \nabla\frac{\partial}{\partial s'} \right)g(\vec{r},\vec{r'})\mathrm{d}s'\qquad(4)\] Здесь интегрирование по всем длинам всех проводников \(L\), \[g(\vec{r},\vec{r'})= \frac{\exp\left({- i k \left|{\vec{r}-\vec{r'}}\right|}\right)}{\left|{\vec{r}-\vec{r'}}\right|},\] \[k = \frac{2\pi\nu}{c},\] \[\eta = \mu_0 c,\]

\(I(s)\) – линейный ток вдоль проводников \(L\), \(s'\) – линейная координата вдоль \(L\), \(\hat{s}\) – единичный вектор вдоль оси проводника в данной точке \(s\), \(\vec{r}\) – координатный вектор точки наблюдения, \(\vec{r'}\) – координатный вектор точки на оси проводника, соответствующей \(s'\), \(\vec{E^I}\) – падающее поле, \(\nu\) – частота излучения, \(\mu_0 = 4\pi \cdot 10^{-7}\) Гн/м – магнитная постоянная, \(c\) – скорость света в вакууме, \(i=\sqrt{-1}\).

Уравнение (4) решается численно при помощи разновидности метода моментов [14]. Каждый диполь разделяется на \(N_s\) прямолинейных цилиндрических частей. Распределение силы тока по длине диполя представляется в виде линейной комбинации \(N_s\) базисных функций \[I(s) = \sum_{j=1}^{N_s} \alpha_j f_j(s),\qquad(5)\] где каждая из базисных функций \(f_j(s)\) задаётся так, что она имеет ненулевые значения только в \(j\)-й и в двух соседних частях диполя (или в \(j\)-й и в одной соседней, если \(j\)–я часть находится у свободного конца диполя), причём в каждой из этих частей \(l\) она имеет вид \[f_j(s) = A_{jl} + B_{jl}\sin(k(s - s_{l})) + C_{jl}\cos(k(s - s_{l})),\] коэффициенты \(A_{jl}\), \(B_{jl}\), \(C_{jl}\) разные в разных частях диполя, причём они находятся из условий, что

• \(f_j(s)\) имеет максимум на \(j\)-й части диполя,

• \[f_j(s_{j+h}+h \Delta_{j+h}/2)=0,\] \[\left.{\frac{\partial f_j(s)}{\partial s}}\right|_{s=s_{j+h}+h \Delta_{j+h}/2}=0,\] \[h=\pm 1,\] т.е. \(f_j(s)\) гладко спадает до нуля на дальних концах соседних (\((j\pm 1)\)-x) частей (части),

• на границах \(j\)-й части диполя с соседними частями (частью) \(f_j(s)\) имеет непрерывные значения и нулевую первую производную, что обеспечивает непрерывность суммарных тока и заряда при любых \(\alpha_j\),

• если \(j\)–я часть диполя находится у его конца, то на этом конце ставится условие \[ f_{j}(s_{j} \pm \Delta_{j}/2) = \frac{\mp 1}{k}\frac{J_{1}(ka)}{J_{0}(ka)} \left.{\frac{\partial f_{j}(s)}{\partial s}}\right|_{s = s_{j} \pm \Delta_{j}/2},\] что при любых \(\alpha_j\) обеспечивает выполнение условия для суммарного тока [15], \[ I(s_{j} \pm \Delta_{j}/2) = \frac{-\left({\hat s_j \cdot \hat n_c}\right)}{k}\frac{J_{1}(ka)}{J_{0}(ka)} \left.{\frac{\partial I(s)}{\partial s}}\right|_{s = s_{j} \pm \Delta_{j}/2},\] учитывающего токи смещения.

  Здесь производные \(\frac{\partial f_j(s)}{\partial s}\), \(\frac{\partial I(s)}{\partial s}\) берутся на свободном конце диполя, \(J_{i}\) – функции Бесселя, \(s_{j}\) – значение \(s\) в центре \(j\)-й части диполя, \(\Delta_j\) – её длина, \(a\) – радиус диполя, \(\hat n_c\) – единичный вектор внешней нормали к торцу диполя, \(\hat s_j\) – единичный вектор вдоль оси \(j\)-й части диполя.

Явные громоздкие формулы для коэффициентов \(A_{jl}\), \(B_{jl}\), \(C_{jl}\) приведены в [16].

Таким образом, уравнение (4) может быть представлено в матричной форме как \[\left[{H}\right] \left[{\alpha }\right]= \left[{E}\right],\qquad(6)\] где \[H_{ij} = \int_S w_i(\vec{r}) \Lambda f_j(\vec{r}) \mathrm{d}S=2\pi a\Lambda f_j(\vec{r}_i),\] \[ \Lambda f(\vec r) = \frac{- i\eta}{4\pi k}\int_{L}^{}f(s') \cdot \left( k^{2}\hat{s}' - \nabla\frac{\partial}{\partial s'} \right)g(\vec{r},\vec{r'})\mathrm{d}s'\] \[E_i = -\int_S w_i(\vec{r})(\hat{s}(\vec{r})\times \vec{E^I}(\vec{r}))\mathrm{d}S = -2\pi a (\hat{s}(\vec{r}_i)\times \vec{E^I}(\vec{r}_i)),\] \[w_i(\vec r) = \delta(\vec r - {\vec r}_i).\]

Здесь \(\Lambda\) – интегральный оператор, действующий на силу тока в правой части уравнения (4), \(a\) – радиус проводников, \(\alpha_j\) – коэффициенты разложения (5), \(w_i\) – весовые функции, \(\delta\) – дельта-функция Дирака, \(\vec{r}_i\) – центры частей диполей, \(S\) – поверхность проводника, \(\mathrm{d}S\) – элемент площади поверхности, \(E_{i}\) – левая часть уравнения (4), рассчитанная в центре \(i\)-й части диполя, матричный элемент \(H_{ij}\) отражает зависимость электрического поля в центре \(i\)-й части диполя от силы тока в \(j\)-й части. Уравнение (6) решается методом Гаусса [17].

После получения распределения токов по \(L\) становится возможным вычисление электрического поля в произвольной точке пространства \(P\) как суммы вкладов от всех частей всех диполей. Вклад \(l\)-й части диполя наиболее просто выражается в соосной ей цилиндрической системе координат \((\hat\rho, \hat\phi, \hat z)\) (\(\rho\) – радиальная, \(\phi\) – азимутальная, \(z\) – осевая компоненты). Пусть координаты \(z\) концов части диполя – \(z_1\) и \(z_2\), и точка \(P\) имеет координаты \((\rho, \phi, z)\). В таком случае, компоненты амплитуды электрического поля \(E^l_\rho, E^l_z\) имеют вид \[ \begin{aligned} E_{\rho}^{l}\left({\rho,z}\right) = & \sum_{j=1}^{N_s} \frac{-\alpha_j}{\lambda} \frac{i\eta}{2k^2} \Bigg( \frac{G_{0}}{\rho} \Bigg\lbrace k(z - z') \left({ B_{jl}\cos(k z') - C_{jl}\sin(k z') }\right) + \\ &+ \left[{1 - \left( z - z' \right)^{2}\left( 1 + {ik}r_{0} \right)\frac{1}{r_{0}^{2}} }\right] \left({ B_{jl}\sin(k z') + C_{jl}\cos(k z') }\right) \Bigg\rbrace \Bigg|_{z_{1}}^{z_{2}} +\\ &+ \rho A_{jl} \left.{\left[{\left( 1 + {ik}r_{0} \right)\frac{G_{0} }{r_{0}^{2}} }\right] }\right|_{z_{1}}^{z_{2}}\Bigg), \end{aligned} \] \[ \begin{aligned} E_z^{l}\left({\rho,z}\right) = & \sum_{j=1}^{N_s} \frac{\alpha_j}{\lambda} \frac{i\eta}{2k^{2}} \Bigg( G_{0} \Bigg\{ k \left({ B_{jl} \cos(k z') - C_{jl}\sin(k z') }\right) - \\ &- \left( 1 + {ik}r_{0} \right)\left( z - z' \right)\frac{1}{r_{0}^{2}} \left({ B_{jl}\sin(k z') + C_{jl} \cos(k z') }\right) \Bigg\} \Bigg|_{z_{1}}^{z_{2}} -\\ &- A_{jl} \left\lbrace{ \left.{\left[{\left(1 + {ik}r_{0} \right)\left( z - z' \right)\frac{G_{0}}{r_{0}^{2}}}\right]}\right|_{z_{1}}^{z_{2}} +k^2\int_{z_1}^{z_2} G_0 dz'}\right\rbrace\Bigg), \end{aligned} \] где \(G_{0} = \exp( - {ik}r_{0})/r_{0}\), \(r_{0} = \sqrt{\rho^{2} + \left( z - z' \right)^{2}}\), \(z_1 < z' < z_2\).

Описанная методика и алгоритм в применении к рассматриваемой задаче – радиофизике облака диполей – в данной постановке учитывает рассеяние излучения, взаимное влияние ближних полей диполей, перенос излучения, эффекты интерференции и др., она предполагает одновременный расчёт взаимозависимых пространственных распределений электромагнитных полей и токов во всех диполях.

1.4 Методика определения радиофизических характеристик облаков диполей

По вышеописанной методике рассчитывалось с помощью пакета прикладных программ “NEC2++” [18] взаимодействие ансамблей из \(N'\) взаимодействующих диполей с электромагнитным излучением. Однако время вычислений нелинейно нарастало с увеличением \(N'\), что существенно затрудняло описание облаков с \(N'\) более нескольких сотен. Очевидно, этого совершенно недостаточно для описания радиофизических свойств анизотропного и неоднородного облака многочисленных диполей. Поэтому на основе указанной методики был принят и обоснован ряд упрощающих приближений.

Вычисления показали, что если же по этой же методике \(N'\) раз определять поле от одиночных диполей указанной формы, то время расчёта многократно сокращалось до уровня, допускающего значения \(N'\) порядка 10000 и более, что уже было бы достаточно для локального статистического описания электрофизических свойств участков облака. Следует отметить, что при этом пренебрегается взаимодействием диполей, т.е. взаимным влиянием их неизлучающихся электрических и магнитных полей в ближних окрестностях диполей. Тогда задача распадается на расчёт взаимодействия с электромагнитным излучением одного рассеивающего диполя и расчёт переноса излучения.

Непосредственное решение уравнения переноса излучения предполагает определение многомерной функции потока электромагнитной энергии в каждый момент времени в каждой точке пространства в каждом направлении распространения волны и для возможных направлений поляризации с рассеянием, что в общем случае также весьма затратно. Поэтому принималось, что влияние соседних диполей на рассеяние падающего излучения данным диполем сводится к экранировке, и пренебрегалось излучением, которое рассеивалось диполями два и более раз. Для определения излучения, выходящего из облака, применялся метод дискретных ординат, причём при расчёте по лучам применялся закон Бугера-Ламберта-Бера.

Для обоснования указанных приближений были проведены тестовые расчёты по упрощённой методике с этими приближениями и по вышеописанной полномасштабной методике (с учётом многократного рассеяния, взаимного влияния диполей друг на друга, интерференции излучения и др.). Задавались координаты и ориентация диполей, для каждой конфигурации проводились вычисления по указанным методам, и набирались статистические данные по отклонению результатов.

Получено практически полное совпадение таких результатов при малой оптической плотности облака диполей \(\tau\) по сравнению с единицей (термин “оптическая плотность” применён с учётом аналогии с характеристиками рассеяния излучения в оптическом диапазоне электромагнитного спектра). Следует отметить, что малость оптической плотности – это формальное условие применимости всех указанных приближений. Т.о., для оптически прозрачных частей облака диполей упрощённая методика точно описывает взаимодействие с электромагнитным полем.

С другой стороны, согласно расчётам, она даёт практически точный результат (отклонения порядка нескольких процентов) и при большой оптической плотности \(\tau \gg 1\).

При \(\tau \approx 1\) для отдельно взятых реализаций наблюдаются значительные (десятки-сотни процентов) отличия между значениями сечений обратного рассеяния по двум указанным методам, но после статистического усреднения эти различия уменьшаются до \(10\ldots 25\%\). Т.о., применяемая методика даёт приемлемую точность и при описании промежуточных значений оптической плотности \(\tau \approx 1\). Отметим, что этот вывод соответствует результатам исследования [19]: после статистического усреднения по конфигурациям экранирование рассеянного излучения является основным фактором влияния диполей друг на друга.

Для большинства рассматриваемых объектов оказались характерными большие перепады оптической плотности по различным частям облака диполей, т.е., как правило, для большей части площади изображения облака характерно выполнение либо условия \(\tau \gg 1\), либо условия \(\tau \ll 1\), для которых данная методика даёт точные результаты. Лишь у меньшей части лучей, формирующих изображение, \(\tau \approx 1\). Для них значения интенсивности рассеянного излучения рассчитываются с погрешностью. Но общая ошибка в интегральном сечении рассеяния невелика. Это является обоснованием применимости вышеуказанных приближений.

Итак, для описания радиофизических свойств облаков, по методике, описанной в разделе 1.1, рассчитывается начальная стадия разлёта компакта диполей, затем, из полученных данных, по методике раздела 1.2 описывается движение такого количества диполей, чтобы оно давало представительную статистическую выборку с точки зрения описания динамики плотности и ориентации диполей в облаке, но требовало приемлемое время вычислений; в расчётном объёме строится регулярная сетка, для каждой ячейки определяются попадающие в неё диполи, и для них по вышеописанной упрощённой методике находятся значения сумм дифференциальных сечений обратного рассеяния для “горизонтальной” и “вертикальной” поляризаций, и сумм интегральных сечений обратного рассеяния. Величины сечений рассеяния затем умножаются на отношение реального количества диполей в облаке к числу траекторий в аэродинамических расчётах. Для каждой ячейки рассчитывается коэффициент отражения (как отношение суммарного сечения обратного рассеяния к площади ячейки в направлении, перпендикулярном направлению распространения падающего излучения) и коэффициент затухания отражённого излучения, обусловленный ненаправленным рассеянием отражённого излучения во всех ячейках, через которые оно проходит.

2 Анализ результатов вычислений

2.1 Динамика, пространственное распределение и ориентация диполей

Проведены серийные расчёты для различных материалов диполей, начальных скоростей, размеров и др. Число индивидуально рассчитываемых траекторий диполей в каждом варианте составляло \(10^4\). Инжекция проводилась в направлении оси \(y\), сила тяжести действовала по отрицательному направлению оси \(z\). Воздух считался неподвижным, плотность его соответствовала нормальным условиям. Начальные координаты разыгрывались с помощью генератора случайных чисел для каждого из диполей в пределах начального объёма в форме усечённого конуса, в котором плотность диполей равна плотности воздуха, а угол образующей конуса и радиальный размер рассчитывались по методике для начальной стадии разлёта (раздел 1.1), как и начальная скорость диполя с учётом торможения и разлёта компакта. Разыгрывались начальная ориентация и форма каждого диполя, т.е. углы отклонения прямолинейных цилиндрических частей, составляющих диполь, от заданной оси. Число таких частей в диполе было 4, углы отклонения находились в пределах \(0\ldots\zeta_\mathrm{max}\). Другие подробности вариантов задания начальных условий указаны ниже. Затем по полученным конфигурациям облаков в характерные моменты времени рассчитывались их радиофизические свойства.

На рис. 1 представлены результаты расчётов для инжекции \(N \approx 10^6\) диполей с основой из стекловолокна, покрытых хорошо проводящим слоем металла, диаметром 10 мкм резонансной длины с начальной скоростью относительно воздуха 200 м/с. Начальная стадия, в соответствии с приведёнными выше данными, длится около 1 мс, причём в её конце диполи тормозятся до скорости в направлении инжекции (по оси \(y\)) около 170 м/с, и расходятся в радиальном направлении примерно на 20 см. В начале следующей стадии диполи считаются хаотически ориентированными и равномерно распределенными в объёме усечённого конуса с радиусами оснований 15 и 20 см и расстоянию между ними 15 см, их скорости считаются равными 170 м/с и направленными по лучам, проходящим через вершину конуса. Т.о., полуугол раскрытия конического потока диполей составляет \(18.5 {^\circ}\).

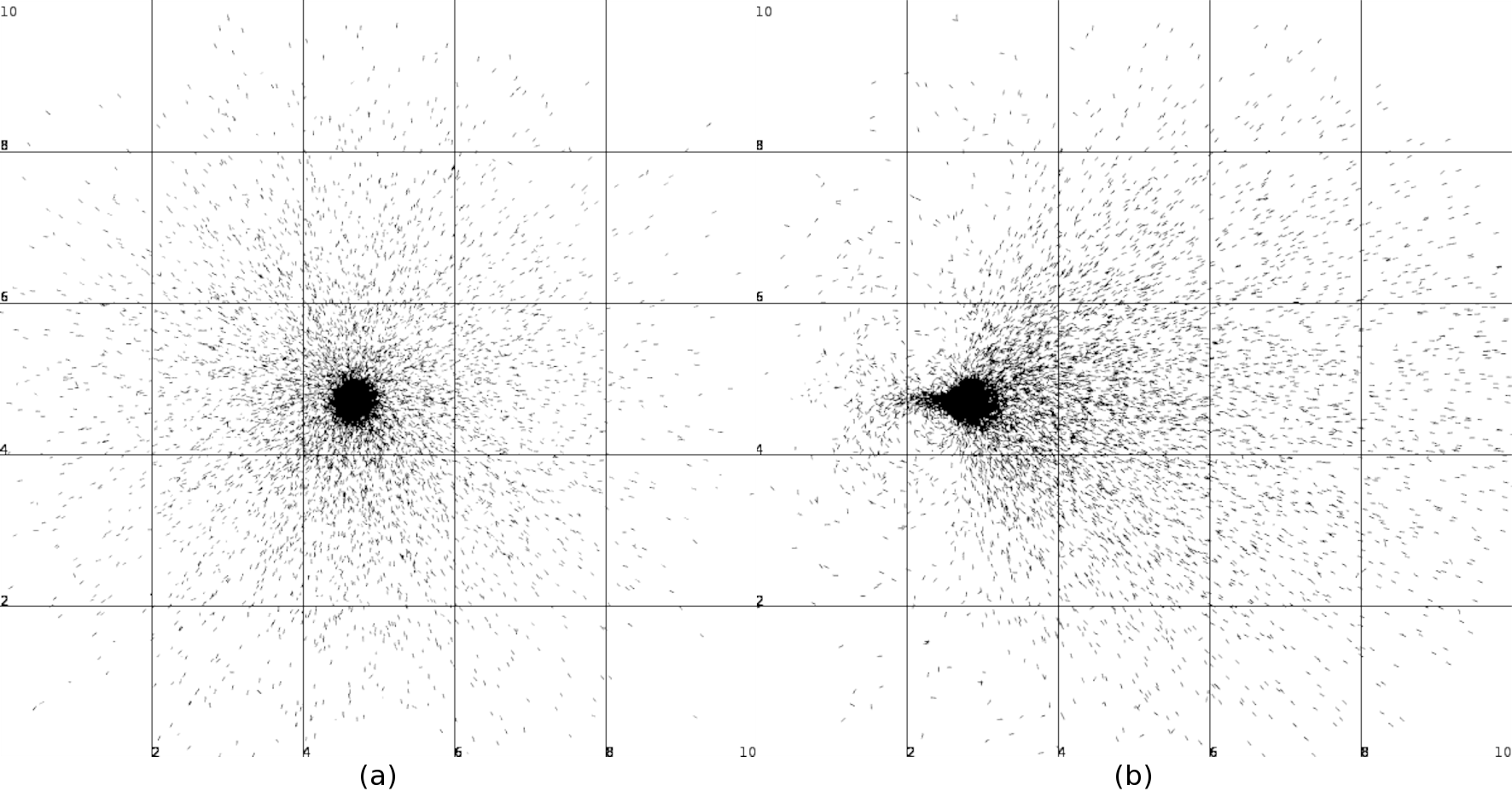
Рассчитывается их независимое движение с учётом инерции и аэродинамических сил и моментов, а также гравитации. Расчёты показали, что кинетическая энергия диполей спадает за несколько десятков миллисекунд, за это же время облако диполей принимает размеры порядка нескольких метров и далее расширяется с гораздо меньшей скоростью. Например, на виде по оси \(x\) в момент времени 50 мс от начала свободного движения диполей размеры облака \(5\times 6\) м, 100 мс – \(8\times 8\) м, 150 мс – \(9\times 10\) м, 200 с – \(10\times 11\) м. В азимутальном направлении облако диполей практически симметрично, что объясняется тем, что инерция и аэродинамические силы в течение рассматриваемого промежутка времени (до 200 мс) преобладают над гравитацией.

Распределение диполей в облаке оказывается резко неоднородным: можно выделить небольшую плотную центральную область и разреженную периферийную (рис. 1). В передней части центральной области ориентация диполей близка к изотропной, а в задней они в основном ориентированы по оси \(y\). Вокруг задней части центральной области наблюдается тороидальная структура, образованная при вращательном движении искривлённых диполей: они то отходят от оси \(y\), то вновь подходят близко к ней, формируя повышенную плотность задней части центральной области. В периферийной области преобладает ориентация диполей, примерно совпадающая с локальной среднемассовой скоростью диполей: это относительно прямолинейные диполи, которые проходят большее расстояние от места инжекции.

2.2 Рассеяние резонансного излучения

Оптическая плотность и интенсивность рассеянного обратно излучения (изображение облака в радиоизлучении) оказываются резко асимметричными в азимутальном направлении, причём оптическая плотность зависит от поляризации падающего излучения (вертикальная, горизонтальная), а интенсивность рассеянного обратно излучения и сечение обратного рассеяния – ещё и от поляризации отражённого излучения (рис. 2(a-c), 3). Это связано с вышеуказанной анизотропией от ориентации диполей.

Количество \(N\) диполей таково, что их суммарное сечение обратного рассеяния \(\sigma_{\Sigma\mathrm{max}}\) для резонансной длины волны при оптической прозрачности облака и хаотической ориентации по (1) составило бы в несколько раз большее значение, чем получаемое в данных расчётах (рис. 4). Причиной этого является экранирование излучения от одних диполей другими диполями. Действительно, оптическая плотность центральной области достигает \(400\ldots 800\) (большие значения для горизонтальной поляризации), а оптическая плотность значительной части периферийной области также превышает единицу. В результате вклады центральной области и задней (относительно зондирующего излучения) части периферийной области в интенсивность рассеянного обратно излучения и общее сечение обратного рассеяния облака оказываются относительно малы, указанные величины в основном определяются процессами в передней (относительно зондирующего излучения) части периферийной области. Её анизотропия вследствие вышеуказанной ориентации диполей обуславливает анизотропию радиофизических свойств облака диполей в целом.

Так как диполи в периферийной области преимущественно ориентированы в направлении оси \(y\) (горизонтальная ось в направлении начального движения диполей относительно воздуха), оптическая плотность в этой области для излучения, идущего вдоль другой горизонтальной оси \(x\), при его горизонтальной поляризации, намного выше, чем для вертикальной поляризации, причём в первом случае значителен вклад передней (относительно движения диполей по воздуху) части облака, а во втором – вклад тороидальных структур и радиальных “потоков” диполей (от центральной области в стороны). В результате при горизонтальной поляризации рассеивающий объём вытянут в горизонтальном направлении, а при вертикальной – в вертикальном. Естественно, это связано с тем, что диполь тем сильнее взаимодействует с излучением, чем ближе его ориентация к направлению поляризации электромагнитной волны.

Картина полностью аналогична для излучения, идущего вдоль вертикальной оси \(z\) (“вид сверху”), вследствие азимутальной симметрии облака диполей.

Для излучения, идущего вдоль горизонтальной оси \(y\), т.е. на “виде спереди”, изолинии оптической плотности вертикально поляризованного излучения также вытянуты по вертикальной оси, а для горизонтально поляризованного излучения – по горизонтальной оси (вследствие указанной ориентации диполей в периферийной области облака). Количественно соответствующие графики при повороте на \(90{^\circ}\) совпадают (из-за азимутальной симметрии облака диполей).

Интенсивность рассеянного обратно излучения зависит как от поляризации падающего излучения (чем ближе направление поляризации электромагнитной волны к ориентации диполя, тем больше сила возбуждаемых в диполе токов), так и от поляризации регистрации рассеянного излучения (диполь излучает рассеянное излучение с направлением поляризации, определяемом его ориентацией). В результате, например, при зондировании горизонтальным радиолучом могут возникать совершенно различные “изображения” облака диполей, если:

1. поляризация падающего излучения горизонтальная, а поляризация регистрации рассеянного излучения – вертикальная (\(yz\));
2. поляризация падающего излучения вертикальная, а поляризация регистрации рассеянного излучения – горизонтальная (\(zy\));
3. поляризация и падающего, и регистрируемого рассеянного излучения горизонтальные (\(yy\));
4. поляризация и падающего, и регистрируемого рассеянного излучения вертикальные (\(zz\)).

Интенсивность рассеянного обратно излучения наибольшая, если совпадают ориентация диполей и поляризация и падающего, и регистрируемого рассеянного излучения. Наиболее близка к этому случаю ситуация, когда излучение приходит по оси \(x\) с горизонтальной (по \(y\)) поляризацией, и регистрируется также горизонтально поляризованное излучение (\(yy\)). Напомним, что диполи в периферийной области преимущественно ориентированы вдоль оси \(y\). Действительно, из результатов расчётов видно, что тогда наиболее велики видимые размеры облака в рассеянном обратно излучении, и сечение обратного рассеяния максимально. Отметим, что из-за отмеченного экранирования центральная область с большой плотностью диполей в данном случае совершенно не видна, форма наиболее интенсивно излучающего объёма образована передней (относительно движения диполей) частью периферийной области и частью тороидальной структуры в задней зоне этой области, а яркость этого объёма близка к яркости белого изотропного рассеивателя.

Для случая вертикальной поляризации излучения (вариант \(zz\)), при его распространении по оси \(x\), интенсивность рассеянного обратно излучения, а также сечение обратного рассеяния примерно вдвое ниже предыдущего случая \(yy\). Центральная зона полностью экранирована. Форма наиболее интенсивно излучающего объёма образована средней (относительно движения диполей) частью периферийной области и другой частью тороидальной структуры в задней зоне этой области, т.е. этот объём вытянут в вертикальном направлении и по форме похож на крылья бабочки.

При вертикальной поляризации излучения (вариант \(zz\)), и его распространении по оси \(y\), рассеяние излучения происходит от передней (относительно движения диполей) части периферийной области облака, обращённой к источнику излучения. В этой части диполи ориентированы преимущественно в направлении от центральной области, т.е. наиболее эффективно с излучением взаимодействуют диполи сверху и снизу, удалённые от оси симметрии облака. Через периферийную зону совершенно не просвечивает центральная, наоборот, в этом месте наблюдается минимум излучения: слишком велика оптическая плотность периферийной области для рассеяния падающего излучения. В результате в регистрируемом отражённом излучении облако диполей выглядит как цифра “8”.

Если направления поляризации падающего и регистрируемого рассеянного излучения перпендикулярны друг другу, то для многих диполей либо малы наводимые излучением токи, либо излучаемые электромагнитные волны не регистрируются из-за другой поляризации. В результате интенсивности рассеянного излучения и сечения обратного рассеяния, например, в вариантах \(xz\) и \(zx\) гораздо ниже, чем для \(xx\) и \(zz\). Наибольший вклад в сигнал приносят диполи, ориентированные под \(45{^\circ}\) к обоим направлениям поляризации. Поэтому, например, так как диполи периферийной области ориентированы преимущественно в направлении от центральной области, то на “виде спереди” облако диполей в вариантах \(xz\) и \(zx\) имеет вид буквы “x”, а на “виде сверху” и “виде сбоку” – как два наклонных луча, выходящие из центральной области под углами \(\pm 45 {^\circ}\) к оси \(y\). Сквозь периферийную область проглядывает центральная область, но общее излучение оттуда относительно мало.

Итак, диполи в описанном варианте формируют облако с высокой оптической плотностью. Поэтому сечение обратного рассеяния во много раз меньше, чем в случае оптически прозрачного облака. На форму и сечение обратного рассеяния значительное влияние оказывает анизотропия ориентации диполей.

2.3 Рассеяние нерезонансного излучения

Проводились также расчёты для нерезонансного излучения. Характерные результаты вычислений для “длинных” диполей длиной \(L = 0.75 \lambda\) представлены на рис. 5.

Оптическая плотность облака диполей в этих случаях значительно меньше, чем для резонансного излучения, но для диполей из металлизированного стекловолокна вначале она всё же значительно превышает единицу не только в центральной области, но и в части периферийной, особенно значительной для направлений “сбоку” и “сверху” (т.е. по осям \(x\) и \(z\)). По мере расширения облака вначале плотная периферийная область становится оптически прозрачной, но в центральной области остаётся \(\tau \gg 1\). На распределениях отражённого излучения поэтому явно видна яркая зона, соответствующая центральной области (рис. 2(d)). Если обратное рассеяние диполями периферийной области близко к максимально возможному при данной ориентации и поляризации излучения, то в центральной области в рассеянии участвуют только диполи, находящиеся со стороны приходящего излучения: излучение остальных диполей центральной области блокировано. Поэтому суммарные сечения рассеяния и в этих случаях ниже, чем при полной оптической прозрачности. Сами значения сечений рассеяния относительно невелики.

2.4 Влияние неопределённости начальных условий

Для оценки надёжности полученных результатов проведён анализ влияния ошибок, связанных с неопределённостью значений малых отклонений формы диполей от прямолинейной, а также приближённостью задания начальных условий независимого движения диполей.

Были проведены вычисления геометрических и радиофизических свойств облаков диполей с вариантом изменённой геометрии начального (для независимого движения диполей) облака: оно задавалось в виде усечённого конуса с диаметрами оснований 12.25 и 25 см (в базовом варианте 10 и 20 см) и расстоянию между ними 10 см (в базовом варианте 15 см), т.е. с полууглом раскрытия конического потока диполей \(31.5{^\circ}\) (в базовом варианте \(18.5 {^\circ}\)). Такое различие с запасом превышает неопределённость угловых характеристик, связанную с приближённостью описания начальной стадии движения, когда воздух испытывает большое возмущение от движения плотного сгустка диполей.

Казалось бы, столь различные начальные диаграммы направленности должны привести к значительному разбросу геометрических и радиофизических свойств облаков диполей. Однако оказалось, что при статистическом усреднении по сложным трёхмерным траекториям диполей различия оказываются не столь велики, и касаются они в основном центральной области, которая, как отмечалось выше, вносит относительно небольшой вклад в радиофизические характеристики. Поэтому неудивительно, что при изменённых начальных условиях сечения обратного рассеяния в начальные моменты времени отличалось от базового варианта примерно на 10% (например, в момент 0.05 с с начала свободного движения диполей и горизонтальной поляризации падающего и рассеянного излучения на “виде слева”, т.е. по оси \(x\), сечение обратного рассеяния было на 10% ниже, а на “виде спереди”, т.е. по оси \(y\) – на 10% выше), а затем и эти небольшие различия практически исчезали. Т.о., острой необходимости в уточнении начальной стадии при свободной инжекции компакта диполей, похоже, нет.

2.5 Влияние формы диполей

Были проведены вычисления геометрических и радиофизических свойств облаков диполей с \(\zeta_\mathrm{max}= 2 {^\circ}\), \(5{^\circ}\) (базовый вариант) и \(8{^\circ}\).

Характерные результаты вычислений представлены на рис. 6.

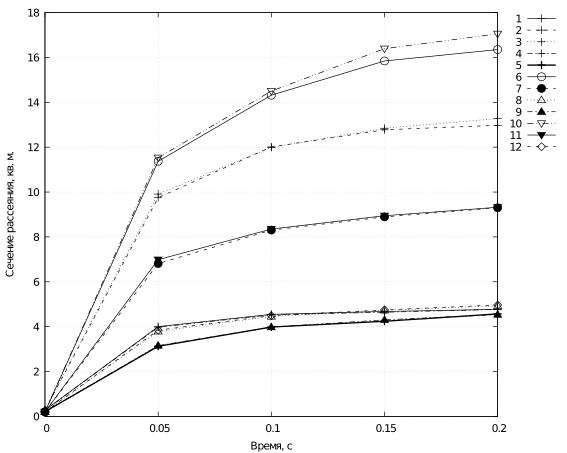
Влияние формы диполей на радиофизические свойства облака оказалось более заметным, чем подробности задания начальных условий свободного движения диполей. Относительно искривлённые диполи с \(\zeta_\mathrm{max}= 8{^\circ}\), например, дают сечение обратного рассеяния, примерно на 20% меньшее, чем с \(\zeta_\mathrm{max}=5{^\circ}\) (базовый вариант), а более прямые, с \(\zeta_\mathrm{max}= 2{^\circ}\) – примерно на 20% большее. Это связано с тем, что более прямые диполи перемещаются по траекториям с меньшей кривизной и большего размера, что приводит к значительному уменьшению количества диполей в центральной области и увеличению в периферийной, при примерном сохранении характерных размеров этих зон. В результате с уменьшением кривизны диполей растёт оптическая плотность наиболее важной для рассеяния излучения периферийной области и площадь оптически плотного отражающего облака, что и даёт рост сечений обратного рассеяния.

Заключение

Проведены вычисления аэродинамики диполей в начале их инжекции в неподвижный воздух, формирование их распределений по пространству, времени и ориентации, изучены радиофизические свойства образующихся облаков диполей.

Показано, что компакт диполей быстро расширяется в первые десятки миллисекунд, образует облако в несколько метров, которое затем относительно медленно увеличивается в размерах. Это облако существенно анизотропно, оно содержит плотную центральную часть и разреженную периферию.

На радиофизические характеристики влияют малые искривления диполей (они определяют траектории и т.о. ориентацию и плотность диполей).

Подписи к рисункам

1. Распределение и ориентация диполей в облаке. Резонансная длина диполя, масштабная сетка в метрах, скорость инжекции 200 м/с, момент времени 200 мс от начала свободного движения, \(\zeta_\mathrm{max}= 5 {^\circ}\). a – вид по оси \(y\), горизонтальная ось \(x\), вертикальная ось \(z\); b – Вид по оси \(x\), горизонтальная ось \(y\), вертикальная ось \(z\)
2. Распределение оптической плотности облака диполей (показано цветом) Резонансная (a-c) и нерезонансная \(0.75 \lambda\) (d) длины диполей, масштабная сетка в метрах, скорость инжекции 200 м/с, момент времени 200 мс от начала свободного движения, \(\zeta_\mathrm{max}= 5 {^\circ}\). a – излучение распространяется вдоль оси \(x\), поляризация по оси \(y\); b – излучение вдоль оси \(x\), поляризация по оси \(z\); c – излучение вдоль оси \(y\), поляризация по оси \(z\); d – нерезонансная длина диполя, аналогично (b)
3. Распределение интенсивности рассеянного обратно излучения, отнесённой к интенсивности падающего излучения (в процентах); масштабная сетка в м. Резонансная длина диполя, \(v_i = 200\) м/с, \(t = 200\) мс, \(\zeta_\mathrm{max}= 5 {^\circ}\). a – падающее излучение вдоль оси \(x\), его поляризация по оси \(y\), поляризация рассеянного излучения по оси \(y\) (xyy); b – (xyz); c – (xzy); d – (xzz); e – (yzx); f – (yzz)
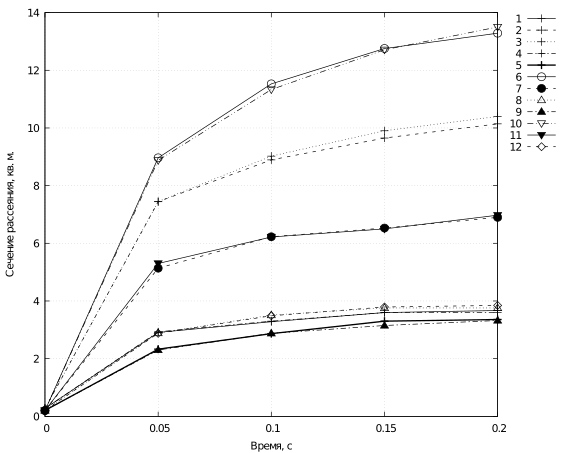
4. Временные зависимости сечений обратного рассеяния, м². Резонансная длина диполя, \(v_i = 200\) м/с, \(\zeta_\mathrm{max}= 5 {^\circ}\). 1 – падающее излучение вдоль оси \(y\), его поляризация по оси \(x\), поляризация рассеянного излучения по оси \(z\) (yxz), 2 – (yxx), 3 – (yzz), 4 – (yzx), 5 – (xyz), 6 – (xyy), 7 – (xzz), 8 – (xzy), 9 – (zyx), 10 – (zyy), 11 – (zxx), 12 – (zxy)
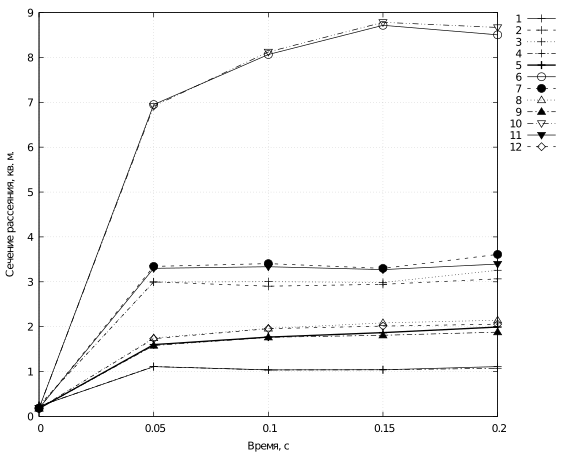
5. Временные зависимости сечений обратного рассеяния, м². Нерезонансная длина диполя \(0.75 \lambda\), \(v_i = 200\) м/с, \(\zeta_\mathrm{max}= 5 {^\circ}\) 1 – падающее излучение вдоль оси \(y\), его поляризация по оси \(x\), поляризация рассеянного излучения по оси \(z\) (yxz), 2 – (yxx), 3 – (yzz), 4 – (yzx), 5 – (xyz), 6 – (xyy), 7 – (xzz), 8 – (xzy), 9 – (zyx), 10 – (zyy), 11 – (zxx), 12 – (zxy)
6. Временные зависимости сечений обратного рассеяния, м². Резонансная длина диполя, \(v_i = 200\) м/с, \(\zeta_\mathrm{max}= 2 {^\circ}\) 1 – падающее излучение вдоль оси y, его поляризация по оси x, поляризация рассеянного излучения по оси z (yxz), 2 – (yxx), 3 – (yzz), 4 – (yzx), 5 – (xyz), 6 – (xyy), 7 – (xzz), 8 – (xzy), 9 – (zyx), 10 – (zyy), 11 – (zxx), 12 – (zxy)

Список литературы