В настоящее время актуальны задачи освоения обширных территорий, в т.ч. районов крайнего Севера, с почти отсутствующей всесезонной дорожной сетью и портовой инфраструктурой при наличии неподготовленной морской береговой линии, болот, рек, озёр и др. Значительную роль в решении этих задач могут сыграть амфибийные средства на воздушной подушке, способные передвигаться как по суше, так и по заболоченным участкам, по мелководью, по глубокой воде [1]. Скорость таких судов при движении по воде должна по возможности превышать критическую (обычно порядка \(20\ldots 40 \;\text{км/ч}\)), тогда энергозатраты на движение значительно снижаются, а дальность автономного передвижения повышается.

Для движителей таких судов традиционно применяются аэродинамические винты и водомёты [2]. Аэродинамические винты при характерных невысоких скоростях транспортного средства (судна) \(v_v\) относительно скорости отбрасываемого воздуха \(v_a\) имеют невысокую эффективность: отношение к потоку энергии \(\frac{1}{2} A \rho v_a^2\) мощности упора (тяги), связанной с силой отдачи от потока импульса \(\frac{1}{2} v_v A \rho v_a\), сравнительно низкое (\(A\) – характерная площадь сечения потока, \(\rho\) – плотность воздуха). Водомётные движители также не свободны от недостатков, в т.ч. [3–6]

• Меньший, по сравнению с винтом, КПД, из-за:
  • Необходимости перевозки, помимо собственно полезного груза, также и воды, находящейся в трубопроводе (в качестве рабочего тела);
  • Потери мощности из-за трения воды в трубопроводах;
  • Потери мощности из-за турбулентных завихрений потока воды в каналах водомёта.
• Затруднительность подачи воды сквозь днище судна к насосу, на эффективность которого будет влиять скорость движения судна относительно воды.
• Водозабор работает также как помпа и может затянуть со дна камни, песок, мусор. Это может забить систему охлаждения либо повредить импеллер и водовод.
• Водометный движитель разрушает дно прибрежной полосы
• Высока степень износа пары ротор-статор, так как эксплуатация производится на мелководье.
• Резкое и внезапное снижение КПД и упора при уменьшении скорости.

В качестве движителей судов применяются гребные колёса с неподвижными или поворотными лопатками (последние меняют угол наклона с частотой циклов поворота, равной частоте оборотов колеса) [7]. Они обеспечивают большой упор при малом заглублении, т.е. применимы на мелководье [8]. При малых скоростях судна \(\boldsymbol{\mathbf{v}}_v\) они отличаются высокой эффективностью, определяемой как отношение мощности, связанной с силой от колеса \(\boldsymbol{\mathbf{F}}\), к механической мощности на валу,

\[\eta = \frac{\boldsymbol{\mathbf{F}}\cdot\boldsymbol{\mathbf{v}}_v}{\left| \boldsymbol{\mathbf{M}} \cdot \boldsymbol{\mathbf{\omega}} \right|},\]

где \(\boldsymbol{\mathbf{M}}\) – вращательный момент на валу, \(\boldsymbol{\mathbf{ω}}\) − угловая скорость вращения колеса.

Длительное время их использование было ограничено [9], что связано, во-первых, с недостаточной надёжностью поворотных лопаток, особенно при высоких скоростях вращения колеса, во-вторых, с тем, что при повышении скорости судна \(v_v\) до \(20\ldots30\;\text{км/ч}\) эффективность движителя \(\eta\) как с поворотными, так и с неподвижными лопатками обычно существенно снижается. Правда, в настоящее время, по-видимому, в связи с достижением предельных характеристик конкурирующих движителей для тихоходных мелкосидящих судов, отмечается некоторый рост интереса к колесным движителям [10; 11].

Принципиальные ограничения эффективности колёсного движителя с неподвижными лопатками при высоких скоростях в литературе практически не описаны. Поэтому представляет значительный интерес изучение и устранение указанных ограничений с целью создания колёсного движителя, эффективного и на высоких, и на низких скоростях судна. Этому и посвящена данная работа.

Решалась система уравнений Навье-Стокса для динамики воздуха и воды как среды с переменной плотностью с учётом силы тяжести и с моделью турбулентности SST (вариант k-ω), в приближении изотермичности и малости числа Маха по сравнению с единицей [12]:

\[ \frac {\partial(r_{\alpha}\rho_{\alpha})} {\partial t} + \nabla \cdot (r_{\alpha} \rho_{\alpha} \boldsymbol{\mathbf{U}}) = 0 \]

\[ \frac {\partial\left( \rho\boldsymbol{\mathbf{U}} \right)} {\partial t} + (\boldsymbol{\mathbf{U}} \cdot \nabla) (\rho\boldsymbol{\mathbf{U}}) - \mu_{eff}\ \Delta\boldsymbol{\mathbf{U}} = \left( \rho - \rho_{ref} \right) \boldsymbol{\mathbf{g}} - \nabla p' \]

\[\mu_{eff} = \mu + \mu_{t}\]

\[p' = p + \frac{2}{3} p k\]

\[\sum_{\alpha}{\nabla \cdot \left( r_{\alpha} \boldsymbol{\mathbf{U}} \right) = 0}\]

\[ \rho = \sum_{\alpha} {r_{\alpha} \rho_{\alpha}}, \] \[ \mu = \sum_{\alpha} {r_{\alpha} \mu_{\alpha}} \]

\[ \frac {\partial\left( \rho k \right)} {\partial t} + \frac {\partial} {\partial x_{j}} \left( \rho U_{j} k \right) = \frac {\partial} {\partial x_{j}} \left\lbrack \left( \mu + \frac{\mu_{t}}{\sigma_{k3}} \right) \frac {\partial k} {\partial x_{j}} \right\rbrack + P_{k} - \beta' \rho k \omega \]

\[ \frac {\partial\left( \rho \omega \right)} {\partial t} + \frac {\partial} {\partial x_{j}} \left( \rho U_{j} \omega \right) = \frac {\partial} {\partial x_{j}} \left\lbrack \left( \mu + \frac{\mu_{t}}{\sigma_{\omega 3}} \right) \frac {\partial\omega} {\partial x_{j}} \right\rbrack + (1 - F_{1}) 2 \rho \frac {1} {\sigma_{\omega 2}\omega} \frac {\partial k} {\partial x_{j}} \frac {\partial\omega} {\partial x_{j}} + a_{3} \frac{\omega}{k} P_{k} - \beta_{3}\rho\omega^{2} \]

\[\mu_{t} = \frac{\rho a_{1} k}{\max\left( a_{1}\omega,SF_{2} \right)}\]

\[P_{k} = \mu_{t}\left( \frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}} \right)\frac{\partial U_{i}}{\partial x_{j}} - \frac{2}{3}\frac{\partial U_{k}}{\partial x_{k}}\left( 3\mu_{t}\frac{\partial U_{k}}{\partial x_{k}} + \rho k \right)\]

\[F_{1} = \tanh{(\xi_{1}^{4})}\]

\[\xi_{1} = \min\left( \xi_{2},\frac{4\rho k}{CD_{kw}\sigma_{\omega 2}y^{2}} \right)\]

\[CD_{kw} = \max\left( 2\rho\frac{1}{\sigma_{\omega 2}\omega}\frac{\partial k}{\partial x_{j}}\frac{\partial\omega}{\partial x_{j}},1.0 \times 10^{- 10} \right)\]

\[\xi_{2} = \max\left( \frac{\sqrt{k}}{\beta' \omega y},\frac{500\mu}{y^{2}\omega\rho} \right)\]

\[F_{2} = \tanh{(\xi_{2}^{2})}\]

Здесь \(\alpha = \lbrace {water},{air}\rbrace\) – индекс, соответствующий воде или воздуху, \(r_{\alpha}\) – объемная доля соответствующей фазы, \(\rho\) – плотность, \(\boldsymbol{\mathbf{U}}\) – вектор скорости среды, t – время, \(\mu_{eff}\) – эффективная вязкость среды, \(\mu\) – динамическая вязкость, \(\mu_{t}\) – турбулентная вязкость, \(\rho_{ref}\) – референсная плотность, \(\rho_{ref} = \rho_{air}\), \(\boldsymbol{\mathbf{g}}\) – вектор ускорения свободного падения, \(k\) – турбулентная кинетическая энергия, \(\omega\) – удельная скорость диссипации, \(P_{k}\) – возникновение турбулентности от вязких сил, S – инвариантная мера скорости деформации, \(F_{1},F_{2}\) – смешивающие функции, \(y\) – расстояние до ближайшей стенки, \(\beta = 0.09\), \(a_{1} = \frac{5}{9}\), \(\beta_{1} = 0.075\), \(\sigma_{k1} = 2\), \(\sigma_{\omega 1} = 2\), \(a_{2} = 0.44\), \(\beta_{2} = 0.0828\), \(\sigma_{k2} = 1\), \(\sigma_{\omega 2} = 1/0.856\) – модельные коэффициенты, \(\Phi_{3} = F_{1}\Phi_{1} + \left( 1 - F_{1} \right)\Phi_{2}\), где \(\Phi = \lbrace a,\ \beta,\ \sigma_{k},\sigma_{\omega}\rbrace\).

Зависимостью параметров от направления вдоль оси вращения пренебрегалось, что хорошо обосновано при характерных условиях, практически устраняющих нежелательные краевые эффекты: при наличии торцевых ограничителей и/или ширине колеса, превышающей ширину лопатки. На одной стороне прямоугольной расчётной области задавались скорости воды и воздуха, равные \(v_v\), постоянное давление воздуха и распределение давления в воде, связанное с гравитацией \(p = \rho_{w} g (H - y)\), где \(H\) – высота уровня воды, \(y\) – вертикальная координата, \(g\) – ускорение свободного падения, \(\rho_{w}\) – плотность воды. На противоположной стороне задавалось свободное истечение с аналогичным распределением давления. На верхней границе задавалось свободное втекание и истечение воздуха \(\nabla \left({\boldsymbol{\mathbf{v}}\cdot\boldsymbol{\mathbf{n}}}\right) = 0\), \(p = p_{0}\), где \(\boldsymbol{\mathbf{v}}\) – скорость среды, \(p\) – давление на границе, \(p_{0}\) – атмосферное давление, \(\boldsymbol{\mathbf{n}}\) – нормаль к границе; на нижней – непротекание \(\boldsymbol{\mathbf{v}}\cdot\boldsymbol{\mathbf{n}} = 0\). Начальные условия соответствовали мгновенному появлению движущегося и вращающегося колеса в покоящихся (в земной системе координат) воде и воздухе. Расчёты производились до установления квазипериодического движения воды и воздуха (более одного оборота колеса).

Применялась подробная квазирегулярная многоблочная расчётная сетка, причём межлопаточные блоки скользили относительно периферийного блока, имеющего форму прямоугольника с вырезанным кругом.

Вычисления проводились с помощью программ ANSYS CFX, для уравнений переноса использовалась численная схема высокого разрешения, для шага по времени обратный метод Эйлера второго порядка, для турбулентности метод первого порядка. В качестве условия сходимости выбрана относительная среднеквадратичная погрешность меньше \(10^{- 4}\). Сила \(\boldsymbol{\mathbf{F}}\) вычислялась как интеграл горизонтальных проекций сил давления и поверхностного трения по всей площади контакта колеса с водой. В качестве параметров воды и воздуха (при \(25\;\text{⁰C}\)) взяты данные из библиотеки материалов ANSYS. При вычислении КПД \(\eta\), проводилось усреднение по времени периода входа лопаток (т.е. оборота колеса, делённого на число лопаток), чтобы сгладить выбросы, связанные с временным сдвигом между продольными импульсами и пиками момента торможения колеса.

Проводились вычислительные эксперименты по математическому моделированию различных вариантов геометрии неподвижных лопаток при скорости судна \(v_v\) от \(10\) до \(45\;\text{км/ч}\) и скорости вращения колеса, соответствующей максимальной окружной скорости \(v_\omega\) от \(10\) до \(60 \;\text{км/ч}\). На приведённых ниже примерах диаметр колеса \(4\;\text{м}\), скорость судна \(v_v = 45\;\text{км/ч}\), \(v_\omega = 60\;\text{км/ч}\).

Вначале был рассмотрен близкий к традиционному (паром ПКР-25, проекты ледоколов и др. [11; 13]) вариант колеса с ободом и радиально расположенными лопатками (вариант I).

Результаты вычислений (рис. 1, 2) показали, что при указанной высокой скорости судна, во-первых, при входе лопатки в воду создаётся большое усилие, сильный всплеск, который гонит воду как назад, так и вперёд. Во-вторых, между лопатками при их нахождении под водой создаётся разрежение, которое формирует течение к колесу, в т.ч., сзади вперёд в земной системе координат. В-третьих, это разрежение замедляет слив воды при выходе лопаток, и вода ускоряется вверх относительно колеса, т.е. вперёд в земной системе координат. Т.о., при движении постоянно происходит захват части воды с ускорением вперёд до скорости порядка \(v_v\). Другая часть воды получает при гребке скорость порядка скорости скольжения \(\Delta v = v_ω − v_v\), но при необходимых высоких скоростях \(\Delta v \ll v_v\). В результате, суммарный импульс, передающийся воде, в среднем направлен вперёд, а не назад, т.е. сила от колеса (упор) направлена назад относительно скорости судна. В результате, при высокой скорости (например, \(v_v = 45 \;\text{км/ч}\)), эффективность движителя не просто мала, а отрицательна: колесо не ускоряет, а тормозит судно (рис. 2).

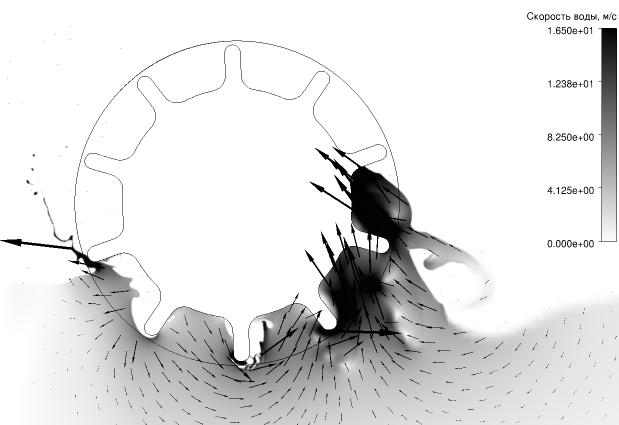
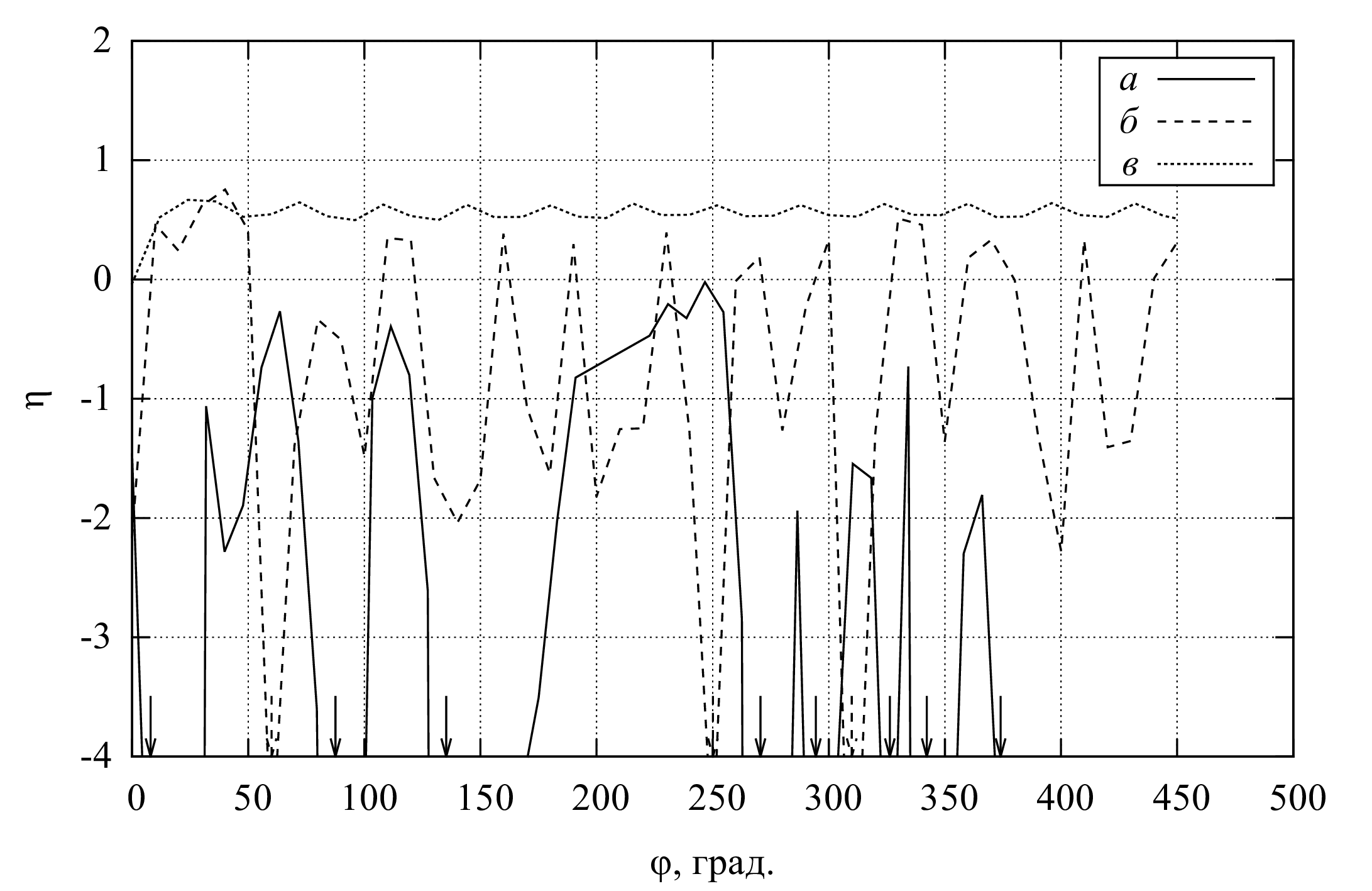
При снижении скорости \(v_v\) до \(10\ldots 15 \;\text{км/ч}\), отрицательные эффекты уменьшаются, и расчётная эффективность \(\eta\) положительна. Отметим, что колёса с такой геометрией лопаток действительно применяются на тихоходных судах.

Другой вариант геометрии (рис. 3) характеризуется лопатками, отделёнными от обода, чтобы давление в межлопаточном пространстве выравнивалось за счёт поступления воздуха со стороны оси вращения (вариант II). По результатам вычислений видно, что эффекты, связанные с разрежением между лопатками, резко ослабляются. Однако при входе лопатки в воду также создаётся большое усилие, локально повышается давление, и формируется течение как назад, так и вперёд. Кроме того, часть воды недостаточно быстро стекает с лопаток и также ускоряется вперёд относительно земной системы координат. В результате при высоких скоростях судна (например, \(v_v = 45 \;\text{км/ч}\)) эффективность движителя оказывается либо недопустимо мала, либо вовсе отрицательна (рис. 2).

В результате анализа вышеуказанного и проведения вариантных вычислений предложена новая геометрия лопаток (вариант III).

Она характеризуется, во-первых, тем, что вместо одиночных лопаток применяются двойные, тройные и пр. лопатки со щелями между ними, через которые вода после гребка сливается с таких лопаток быстрее, чем с одиночных лопаток. Это обеспечивает снижение массы ускоряемой вперёд воды и соответствующей отрицательной составляющей силы, действующей на колесо.

Во-вторых, тем, что внешняя лопатка имеет такой угол наклона относительно соответствующего радиуса, что при заданных \(v_v\) и \(v_\omega\) её внешний край входил бы в неподвижную воду под нулевым углом атаки. Это условие на угол атаки, характерное для оптимальных режимов практически всех лопаточных машин, обеспечивает снижение потерь импульса при входе лопатки в воду.

В-третьих, внутренние лопатки так расположены относительно внешних, что вода, текущая при гребке вдоль внешней лопатки со стороны повышенного давления, проходит по инерции мимо межлопаточной щели и попадает на поверхность внутренней лопатки. Это обеспечивает снижение потерь импульса при гребке из-за протекания воды по щелям.

В-четвёртых, углы наклона внутренних лопаток таковы, что стекающие с внешних лопаток потоки воды, имеющие значительную вертикальную составляющую, направляются внутренними лопатками горизонтально назад. Это снижает потери импульса на вертикальную составляющую.

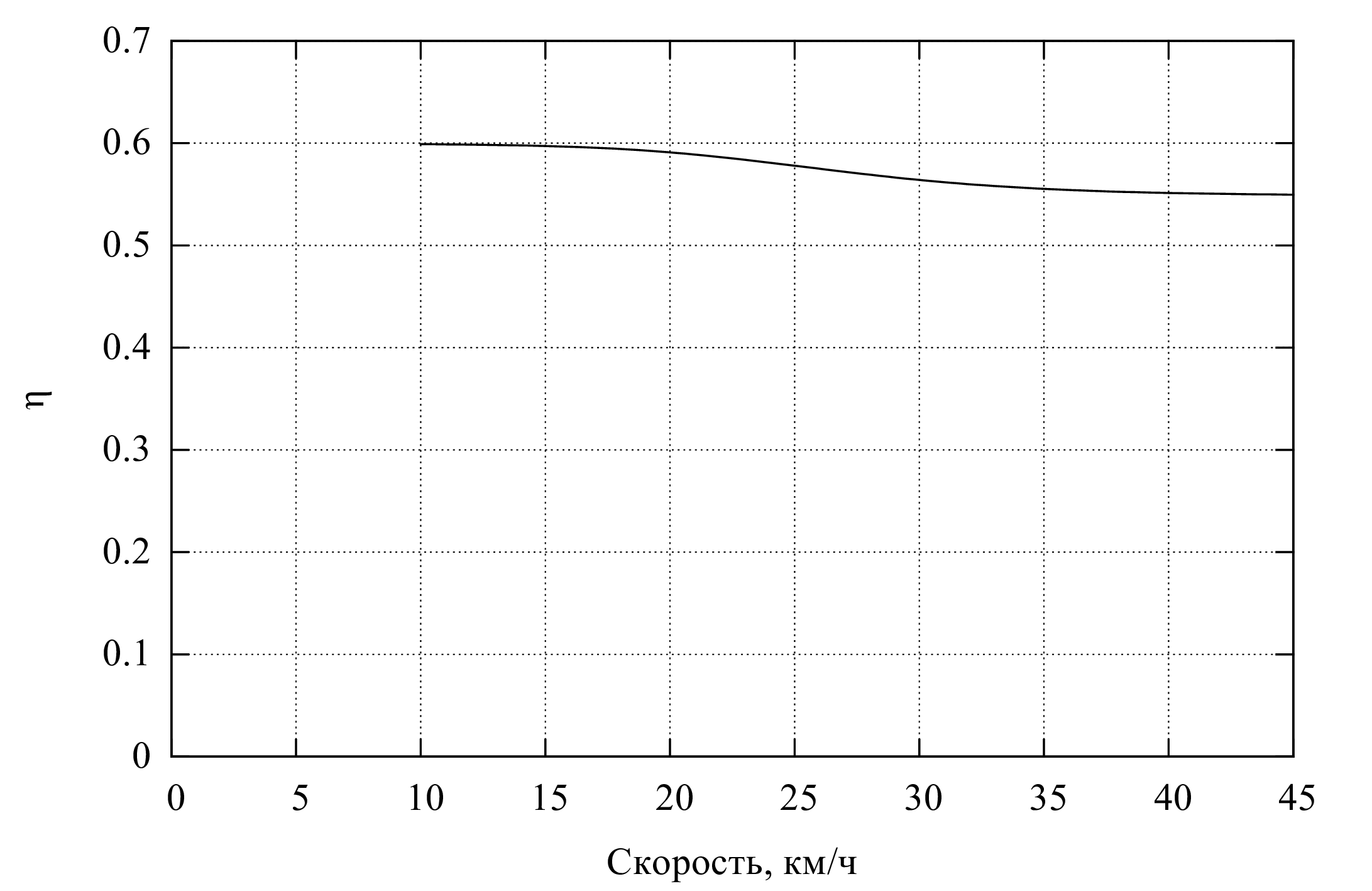
Результаты вычислений для лопаток с новой геометрией представлены на рис. 2, 4, 5.

Видно, что, несмотря на то, что воду в месте входа лопатки нельзя назвать неподвижной, погружение происходит без значительного всплеска и без локального повышения давления. Это минимизирует потери на вход.

Вода действительно меньше захватывается и быстрее сливается с нескольких коротких лопаток, чем с одной длинной, что снижает массу захватываемой воды и соответствующие потери импульса.

В то же время, при гребке протекание воды по щелям указанной геометрии затруднено из-за инерционности потоков воды, которые для этого должны поворачивать со значительными ускорениями. Поэтому, как и при сплошных лопатках, создаётся тянущее воду пониженное давление за разрезной лопаткой, а также толкающее воду повышенное давление перед лопаткой. В результате разрезные лопатки обеспечивают эффективность ускорения воды назад. Т.о., щели указанной геометрии не снижают создаваемый упор.

Вертикальная составляющая скорости движения воды, возникающая при гребке после взаимодействия с нижними лопатками, при взаимодействии с верхними лопатками эффективно преобразуется в горизонтальную, что увеличивает горизонтальную составляющую импульса, направленную назад относительно скорости судна, и повышает эффективность движителя.

Видно, что в результате принятых мер гребное колесо оказывается высокоэффективным движителем при высоких скоростях движения судна: значение \(\eta\) при скорости судна \(v_v = 45 \;\text{км/ч}\) достигает \(55\%\). Кроме того, при меньших \(v_v\) оно оказывается даже несколько более эффективно– при условии сохранения вышеописанного соотношения между \(v_v\) и \(v_\omega\), обеспечивающего плавный вход в воду (рис. 5).

Т.о., гребное колесо новой конструкции обладает качествами, критически важными для применения, в т.ч., в условиях Крайнего Севера. Значительный интерес представляет разработка движителей с применением гребных колес для вновь создаваемых судов амфибийного типа.

Список литературы